命題p:?x∈[1,2],x2-a≥0,命題q:方程x2+(2a-1)x+a2=0有兩個大于1的不相等的根.若命題p或q是真命題,p且q是假命題,求實數a的取值范圍.
【答案】
分析:根據一元二次方程根的個數與△的關系,我們可以求出命題p及命題q為真時,參數a的取值范圍,
進而根據p或q為真命題,p且q為假命題,可知命題p與命題q中一個為真,一個為假,進而分類討論后,即可得到答案.
解答:解:由于命題p:?x∈[1,2],x
2-a≥0,
命題q:方程x
2+(2a-1)x+a
2=0有兩個大于1的不相等的根.
則命題p:a≤1,
命題q:
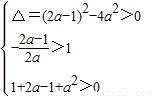
⇒a<-2.
又由p或q為真命題,p且q為假命題,
可知命題p與命題q中一個為真,一個為假,
當p真q假時,
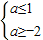
∴-2≤a≤1;
當p假q真時,
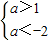
∴a∈∅.
綜上可知,實數a的取值范圍為-2≤a≤1.
點評:本題考查的知識點是命題的真假判斷與應用,其中根據一元二次方程根的個數與△的關系,分別求出命題p為真命題時,及命題q為真時,參數a的取值范圍,是解答本題的關鍵.

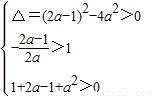 ⇒a<-2.
⇒a<-2.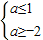 ∴-2≤a≤1;
∴-2≤a≤1;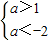 ∴a∈∅.
∴a∈∅.
