
分析 (1)極坐標方程兩邊同乘ρ,再用極坐標和直角坐標互化方程組$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$和$\left\{\begin{array}{l}{{ρ}^{2}={x}^{2}+{y}^{2}}\\{tanθ=\frac{y}{x}}\end{array}\right.$轉化為x,y的關系式,即可.
(2)利用直線的參數方程中參數的幾何意義求解.將參數方程代入曲線C1,得關于t的一元二次方程,再結合韋達定理求解|EA|+|EB|所表達出的韋達定理的結構式.因E在曲線C1(圓)內,故|EA|+|EB|=|AB|,也可以直接轉化為直角坐標系下普通方程,求直線與圓的弦長|AB|.
解答 解:(1)曲線C1的極坐標方程為ρ=2(cosθ+sinθ),
兩邊同乘乘ρ,得ρ2=2(ρcosθ+ρsinθ)
∵$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$ 且 ρ2=x2+y2
∴曲線C1的直角坐標方程為 x2+y2=2x+2y 即(x-1)2+(y-1)2=2 …2分
曲線C2的參數方程為$\left\{\begin{array}{l}{x=2cosα}\\{y=-sinα}\end{array}\right.$ (α為參數)則$\left\{\begin{array}{l}{cosα=\frac{x}{2}}\\{sinα=-y}\end{array}\right.$
∵cos2α+sin2α=1
∴曲線C2的直角坐標方程為 $\frac{{x}^{2}}{4}+{y}^{2}=1$ …4分
(2)解法一:
直線l:$\left\{\begin{array}{l}{x=\frac{1}{2}t}\\{y=1+\frac{\sqrt{3}}{2}t}\end{array}\right.$(t為參數)與y軸交點為E(0,1)…5分
直線l與曲線C1交于A,B兩點,由直線l參數t的意義
知|EA|+|EB|=|tA|+|tB|…6分
將直線l參數方程代入曲線C1直角坐標方程
得:$(\frac{1}{2}t-1)^{2}+(1+\frac{\sqrt{3}}{2}t-1)^{2}=2$ 即 t2-t-1=0
∴tA+tB=1,tAtB=-1 …8分
因為E(0,1)在曲線C1內,
∴|EA|+|EB|=|tA|+|tB|=|tA-tB|
=$\sqrt{({t}_{A}+{t}_{B})^{2}-4{t}_{A}{t}_{B}}$
=$\sqrt{5}$. …10分
解法二:直線l的普通方程為$y=\sqrt{3}x+1$ …5分
由(1)知曲線C1是以(1,1)為圓心,以$\sqrt{2}$為半徑的圓.
因E在圓C1內,∴|EA|+|EB|=|AB|…6分
又∵圓心(1,1)到直線l的距離d=$\frac{|\sqrt{3}-1+1|}{\sqrt{{\sqrt{3}}^{2}+{1}^{2}}}$=$\frac{\sqrt{3}}{2}$ …8分
∴|AB|=$2\sqrt{{\sqrt{2}}^{2}-(\frac{\sqrt{3}}{2})^{2}}$=$\sqrt{5}$,
∴|EA|+|EB|=$\sqrt{5}$. …10分
點評 考查極坐標方程化直角坐標方程,參數方程化普通方程,直線參數方程的意義.考查方程思想.屬于中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
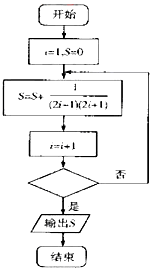
| A. | i>2014 | B. | i>2014 | C. | i>2015 | D. | i>2017 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 把正整數按一定的規則排成了如圖所示的三角形數表,設aij(i,j∈N*)是位于這個三角形數表中從上往下數第i行,從左往右數第j個數,如a63=18,若aij=2012,則i+j=( )
把正整數按一定的規則排成了如圖所示的三角形數表,設aij(i,j∈N*)是位于這個三角形數表中從上往下數第i行,從左往右數第j個數,如a63=18,若aij=2012,則i+j=( )| A. | 75 | B. | 76 | C. | 77 | D. | 78 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com