
【題目】如圖,已知菱形![]() 與直角梯形
與直角梯形![]() 所在的平面互相垂直,其中
所在的平面互相垂直,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點
的中點
(Ⅰ)求證:![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)設![]() 為線段
為線段![]() 上一點,
上一點,![]() ,若直線
,若直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,求
,求![]() 的長.
的長.
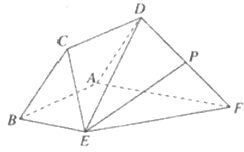
【答案】(Ⅰ)見解析;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
試題
(Ⅰ)要證線面平行,就要證線線平行,考慮到![]() 是
是![]() 中點,因此取
中點,因此取![]() 中點
中點![]() ,可得
,可得![]() 與
與![]() 平行且相等,從而可證得
平行且相等,從而可證得![]() ,所以可證得線面平行;
,所以可證得線面平行;
(Ⅱ)求二面角,可建立空間直角坐標系,用向量法求解,考慮到平面![]() 與平面
與平面![]() 垂直,
垂直,![]() 是菱形,因此取
是菱形,因此取![]() 中點
中點![]() ,則有
,則有![]() ,因此
,因此![]() ,所以可作
,所以可作![]() ,以
,以![]() 為
為![]() 軸建立空間直角坐標系,寫出各點坐標,求出二面角兩個面的法向量,由法向量的夾角可得二面角;
軸建立空間直角坐標系,寫出各點坐標,求出二面角兩個面的法向量,由法向量的夾角可得二面角;
(Ⅲ)在(Ⅱ)的坐標系,利用已知![]() 得
得![]() 點坐標,從而可得向量
點坐標,從而可得向量![]() 的坐標,利用向量
的坐標,利用向量![]() 與平面
與平面![]() 的法向量夾角的正弦值可求得
的法向量夾角的正弦值可求得![]() ,最后可得
,最后可得![]() 的長度.
的長度.
試題解析:
(Ⅰ)取![]() 的中點
的中點![]() ,連接
,連接![]() ,則
,則![]() ∥
∥![]() ∥
∥![]() ,且
,且![]() ,所以四邊形
,所以四邊形![]() 為平行四邊形
為平行四邊形
所以![]() ∥
∥![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
則![]() ∥平面
∥平面![]() .
.
(Ⅱ)取![]() 中點
中點![]() ,連接
,連接![]() ,則
,則![]() 因為平面
因為平面![]()
![]() 平面
平面![]() ,交線為
,交線為![]() ,則
,則![]() 平面
平面![]()
作![]() ∥
∥![]() ,分別以
,分別以![]() 所在直線為
所在直線為![]() 軸建立空間直角坐標系,如圖,
軸建立空間直角坐標系,如圖,

則![]()
于是![]() ,設平面
,設平面![]() 的法向量
的法向量![]() ,
,
則![]() 令
令![]() ,則
,則![]()
平面![]() 的法向量
的法向量![]()
所以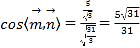
又因為二面角![]() 為銳角,所以其余弦值為
為銳角,所以其余弦值為![]() .
.
(Ⅲ)![]() 則
則![]() ,
,
![]() ,而平面
,而平面![]() 的法向量為
的法向量為![]() ,
,
設直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,
,
于是![]()
于是![]() ,
,![]() .
.


科目:高中數學 來源: 題型:
【題目】“五一”期間,甲乙兩個商場分別開展促銷活動.
(Ⅰ)甲商場的規則是:凡購物滿100元,可抽獎一次,從裝有大小、形狀相同的4個白球、4個黑球的袋中摸出4個球,中獎情況如下表:
摸出的結果 | 獲得獎金(單位:元) |
4個白球或4個黑球 | 200 |
3個白球1個黑球或3個黑球1個白球 | 20 |
2個黑球2個白球 | 10 |
記![]() 為抽獎一次獲得的獎金,求
為抽獎一次獲得的獎金,求![]() 的分布列和期望.
的分布列和期望.
(Ⅱ)乙商場的規則是:凡購物滿100元,可抽獎10次.其中,第![]() 次抽獎方法是:從編號為
次抽獎方法是:從編號為![]() 的袋中(裝有大小、形狀相同的
的袋中(裝有大小、形狀相同的![]() 個白球和
個白球和![]() 個黑球)摸出
個黑球)摸出![]() 個球,若該次摸出的
個球,若該次摸出的![]() 個球顏色都相同,則可獲得獎金
個球顏色都相同,則可獲得獎金![]() 元;記第
元;記第![]() 次獲獎概率
次獲獎概率![]() .設各次摸獎的結果互不影響,最終所獲得的總獎金為10次獎金之和.
.設各次摸獎的結果互不影響,最終所獲得的總獎金為10次獎金之和.
①求證:![]() ;
;
②若某顧客購買120元的商品,不考慮其它因素,從獲得獎金的期望分析,他應該選擇哪一家商場?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校為了普及環保知識,增強學生的環保意識,在全校組織了一次有關環保知識的競賽.經過初賽、復賽,甲、乙兩個代表隊(每隊3人)進入了決賽,規定每人回答一個問題,答對為本隊贏得10分,答錯得0分.假設甲隊中每人答對的概率均為![]() ,乙隊中3人答對的概率分別為
,乙隊中3人答對的概率分別為![]() ,
,![]() ,
,![]() ,且各人回答正確與否相互之間沒有影響,用
,且各人回答正確與否相互之間沒有影響,用![]() 表示乙隊的總得分.
表示乙隊的總得分.
(Ⅰ)求![]() 的分布列及數學期望;
的分布列及數學期望;
(Ⅱ)求甲、乙兩隊總得分之和等于30分且甲隊獲勝的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某單位甲、乙、丙三個部門的員工人數分別為24,16,16.現采用分層抽樣的方法從中抽取7人,進行睡眠時間的調查.
(I)應從甲、乙、丙三個部門的員工中分別抽取多少人?
(II)若抽出的7人中有4人睡眠不足,3人睡眠充足,現從這7人中隨機抽取3人做進一步的身體檢查.
(i)用X表示抽取的3人中睡眠不足的員工人數,求隨機變量X的分布列與數學期望;
(ii)設A為事件“抽取的3人中,既有睡眠充足的員工,也有睡眠不足的員工”,求事件A發生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某科研小組研究發現:一棵水蜜桃樹的產量![]() (單位:百千克)與肥料費用
(單位:百千克)與肥料費用![]() (單位:百元)滿足如下關系:
(單位:百元)滿足如下關系:![]() ,且投入的肥料費用不超過5百元.此外,還需要投入其他成本(如施肥的人工費等)
,且投入的肥料費用不超過5百元.此外,還需要投入其他成本(如施肥的人工費等)![]() 百元.已知這種水蜜桃的市場售價為16元/千克(即16百元/百千克),且市場需求始終供不應求.記該棵水蜜桃樹獲得的利潤為
百元.已知這種水蜜桃的市場售價為16元/千克(即16百元/百千克),且市場需求始終供不應求.記該棵水蜜桃樹獲得的利潤為![]() (單位:百元).
(單位:百元).
(1)求利潤函數![]() 的函數關系式,并寫出定義域;
的函數關系式,并寫出定義域;
(2)當投入的肥料費用為多少時,該水蜜桃樹獲得的利潤最大?最大利潤是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com