
| MA |
| AN |
| MB |
| BN |
|
|
|
|


 新思維小冠軍100分作業本系列答案
新思維小冠軍100分作業本系列答案 名師指導一卷通系列答案
名師指導一卷通系列答案科目:高中數學 來源: 題型:
若給定橢圓C:ax2+by2=1(a>0,b>0,a![]() b)和點N(x0,y0),則稱直線l:ax0x+by0y=1為橢圓C的“伴隨直線”,
b)和點N(x0,y0),則稱直線l:ax0x+by0y=1為橢圓C的“伴隨直線”,
(1)若N(x0,y0)在橢圓C上,判斷橢圓C與它的“伴隨直線”的位置關系(當直線與橢圓的交點個數為0個、1個、2個時,分別稱直線與橢圓相離、相切、相交),并說明理由;
(2)命題:“若點N(x0,y0)在橢圓C的外部,則直線l與橢圓C必相交.”寫出這個命題的逆命題,判斷此逆命題的真假,說明理由;
(3)若N(x0,y0)在橢圓C的內部,過N點任意作一條直線,交橢圓C于A、B,交l于M點(異于A、B),設![]() ,
,![]() ,問
,問![]() 是否為定值?說明理由.
是否為定值?說明理由.
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| MA |
| AN |
| MB |
| BN |
查看答案和解析>>
科目:高中數學 來源:2008年上海市上海中學高三3月綜合練習數學試卷1(文理合卷)(解析版) 題型:解答題
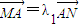 ,
,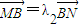 ,問λ1+λ2是否為定值?說明理由.
,問λ1+λ2是否為定值?說明理由.查看答案和解析>>
科目:高中數學 來源:2010年上海市上海中學高三數學綜合練習試卷(1)(解析版) 題型:解答題
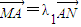 ,
,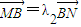 ,問λ1+λ2是否為定值?說明理由.
,問λ1+λ2是否為定值?說明理由.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com