
 時,不等式
時,不等式 成立;
成立; 成立,能否將條件“
成立,能否將條件“ ”適當放寬?若能,請放寬條件并簡述理由;若不能,也請說明理由;
”適當放寬?若能,請放寬條件并簡述理由;若不能,也請說明理由; 且
且 ,式子
,式子 與
與 同號,恒成立,
同號,恒成立, 且
且 .
. 且
且 ,
, ,
, ,
, .
.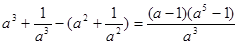 ,
, ,
, 
 ,
, 成立.
成立. 且
且 ,式子
,式子 與
與 同號,恒成立,
同號,恒成立, 且
且 .
. 且
且 ,
, ,
, ,
, .
.
 .
. ,則由
,則由 不等式成立;
不等式成立; ,則由
,則由 不等式成立.
不等式成立. 且
且 ,
, ,
, ,
, 成立.
成立. 且
且 ,
, ,
, 也對.
也對.

 能力評價系列答案
能力評價系列答案 唐印文化課時測評系列答案
唐印文化課時測評系列答案 導學與測試系列答案
導學與測試系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com