
【題目】已知函數![]() ,其中
,其中![]() ,
, ![]() 是自然對數的底數.
是自然對數的底數.
(1)當![]() 時,求曲線
時,求曲線![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)求函數![]() 的單調減區間;
的單調減區間;
(3)若![]() 在
在![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() (2)當
(2)當![]() 時,
時, ![]() 無單調減區間;當
無單調減區間;當![]() 時,
時, ![]() 的單調減區間是
的單調減區間是![]() ;當
;當![]() 時,
時, ![]() 的單調減區間是
的單調減區間是![]() .(3)
.(3)![]()
【解析】試題分析:(1)先對函數解析式進行求導,再借助導數的幾何意義求出切線的斜率,運用點斜式求出切線方程;(2)先對函數的解析式進行求導,然后借助導函數的值的符號與函數單調性之間的關系進行分類分析探求;(3)先不等式![]() 進行等價轉化,然后運用導數知識及分類整合的數學思想探求函數的極值與最值,進而分析推證不等式的成立求出參數的取值范圍。
進行等價轉化,然后運用導數知識及分類整合的數學思想探求函數的極值與最值,進而分析推證不等式的成立求出參數的取值范圍。
解:(1)因為![]() ,所以
,所以![]() .
.
因為![]() ,所以
,所以![]() .
.
所以切線方程為![]() .
.
(2) 因為![]() ,
,
當![]() 時,
時, ![]() ,所以
,所以![]() 無單調減區間.
無單調減區間.
當![]() 即
即![]() 時,列表如下:
時,列表如下:

所以![]() 的單調減區間是
的單調減區間是![]() .
.
當![]() 即
即![]() 時,
時, ![]() ,列表如下:
,列表如下:
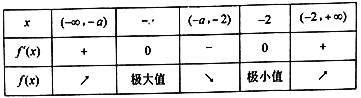
所以![]() 的單調減區間是
的單調減區間是![]() .
.
綜上,當![]() 時,
時, ![]() 無單調減區間;
無單調減區間;
當![]() 時,
時, ![]() 的單調減區間是
的單調減區間是![]() ;
;
當![]() 時,
時, ![]() 的單調減區間是
的單調減區間是![]() .
.
(3) ![]() .
.
當![]() 時,由(2)可得,
時,由(2)可得, ![]() 為
為![]() 上單調增函數,
上單調增函數,
所以![]() 在區間
在區間![]() 上的最大值
上的最大值![]() ,符合題意.
,符合題意.
當![]() 時,由(2)可得,要使
時,由(2)可得,要使![]() 在區間
在區間![]() 上恒成立,
上恒成立,
只需![]() ,
, ![]() ,解得
,解得![]() .
.
當![]() 時,可得
時,可得![]() ,
, ![]() .
.
設![]() ,則
,則![]() ,列表如下:
,列表如下:

所以![]() ,可得
,可得![]() 恒成立,所以
恒成立,所以![]() .
.
當![]() 時,可得
時,可得![]() ,無解.
,無解.
綜上, ![]() 的取值范圍是
的取值范圍是![]() .
.


 字詞句篇與同步作文達標系列答案
字詞句篇與同步作文達標系列答案科目:高中數學 來源: 題型:
【題目】在長方體ABCD﹣A1B1C1D1中,B1 C和C1D與底面A1B1C1D1所成的角分別為60°和45°,則異面直線B1C和C1D所成角的余弦值為( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4—4:坐標系與參數方程。
在平面直角坐標系![]() 中,已知曲線
中,已知曲線![]()
![]() ,以平面直角坐標系
,以平面直角坐標系![]() 的原點
的原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸,取相同的單位長度建立極坐標系,已知直線
軸的正半軸為極軸,取相同的單位長度建立極坐標系,已知直線![]() .
.
(1)將曲線![]() 上的所有點的橫坐標、縱坐標分別伸長為原來的
上的所有點的橫坐標、縱坐標分別伸長為原來的![]() 、2倍后得到曲線
、2倍后得到曲線![]()
試寫出直線![]() 的直角坐標方程和曲線
的直角坐標方程和曲線![]() 的參數方程;
的參數方程;
(2)在曲線![]() 上求一點
上求一點![]() ,使點
,使點![]() 到直線
到直線![]() 的距離最大,并求出此最大值.
的距離最大,并求出此最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com