
【題目】已知過點M( ![]() ,0)的直線l與拋物線y2=2px(p>0)交于A,B兩點,且
,0)的直線l與拋物線y2=2px(p>0)交于A,B兩點,且 ![]() =﹣3,其中O為坐標原點.
=﹣3,其中O為坐標原點.
(1)求p的值;
(2)當|AM|+4|BM|最小時,求直線l的方程.
【答案】
(1)解:設A(x1,y1),Bx2,y2),直線l:x=my+ ![]() ,
,
代入拋物線方程,消去x,得,y2﹣2pmy﹣p2=0,
y1+y2=2pm,y1y2=﹣p2,
由于 ![]() =﹣3,即x1x2+y1y2=﹣3,
=﹣3,即x1x2+y1y2=﹣3,
x1x2= ![]() =
= ![]() ,
,
即有 ![]() ﹣p2=﹣3,解得,p=2
﹣p2=﹣3,解得,p=2
(2)解:由拋物線的定義,可得,|AM|=x1+1,|BM|=x2+1,
則|AM|+4|BM|=x1+4x2+5 ![]() +5=9,
+5=9,
當且僅當x1=4x2時取得最小值9.
由于x1x2=1,則解得,x2= ![]() (負的舍去),
(負的舍去),
代入拋物線方程y2=4x,解得,y2= ![]() ,即有B(
,即有B( ![]() ),
),
將B的坐標代入直線x=my+1,得m= ![]() .
.
則直線l:x= ![]() y+1,即有4x+
y+1,即有4x+ ![]() y﹣4=0或4x﹣
y﹣4=0或4x﹣ ![]() y﹣4=0
y﹣4=0
【解析】(1)設A(x1 , y1),Bx2 , y2),直線l:x=my+ ![]() ,代入拋物線方程,運用韋達定理,及平面向量的數量積的坐標表示,即可得到p=2;(2)運用拋物線的定義,及均值不等式,即可得到最小值9,注意等號成立的條件,求得B的坐標,代入直線方程,求得m,即可得到直線l的方程.
,代入拋物線方程,運用韋達定理,及平面向量的數量積的坐標表示,即可得到p=2;(2)運用拋物線的定義,及均值不等式,即可得到最小值9,注意等號成立的條件,求得B的坐標,代入直線方程,求得m,即可得到直線l的方程.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】設F(x)=f(x)+f(﹣x)在區間 ![]() 是單調遞減函數,將F(x)的圖象按向量
是單調遞減函數,將F(x)的圖象按向量 ![]() 平移后得到函數G(x)的圖象,則G(x)的一個單調遞增區間是( )
平移后得到函數G(x)的圖象,則G(x)的一個單調遞增區間是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4―4:坐標系與參數方程]
在直角坐標系xOy中,曲線C的參數方程為![]() (θ為參數),直線l的參數方程為
(θ為參數),直線l的參數方程為![]() .
.
(1)若a=1,求C與l的交點坐標;
(2)若C上的點到l的距離的最大值為![]() ,求a.
,求a.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于函數f(x)=2sin(3x﹣ ![]() ),有下列命題:①其表達式可改寫為y=2cos(3x﹣
),有下列命題:①其表達式可改寫為y=2cos(3x﹣ ![]() );②y=f(x)的最小正周期為
);②y=f(x)的最小正周期為 ![]() ;③y=f(x)在區間(
;③y=f(x)在區間( ![]() ,
, ![]() )上是增函數;④將函數y=2sin3x的圖象上所有點向左平行移動
)上是增函數;④將函數y=2sin3x的圖象上所有點向左平行移動 ![]() 個單位長度就得到函數y=f(x)的圖象.其中正確的命題的序號是(注:將你認為正確的命題序號都填上).
個單位長度就得到函數y=f(x)的圖象.其中正確的命題的序號是(注:將你認為正確的命題序號都填上).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一條寬為![]() 的兩平行河岸有村莊
的兩平行河岸有村莊![]() 和供電站
和供電站![]() ,村莊
,村莊![]() 與
與![]() 的直線距離都是
的直線距離都是![]() ,
, ![]() 與河岸垂直,垂足為
與河岸垂直,垂足為![]() 現要修建電纜,從供電站
現要修建電纜,從供電站![]() 向村莊
向村莊![]() 供電.修建地下電纜、水下電纜的費用分別是
供電.修建地下電纜、水下電纜的費用分別是![]() 萬元
萬元![]() 、
、![]() 萬元
萬元![]() .
.
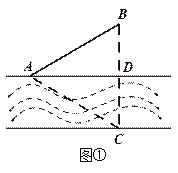
(1) 如圖①,已知村莊![]() 與
與![]() 原來鋪設有電纜
原來鋪設有電纜![]() ,現先從
,現先從![]() 處修建最短水下電纜到達對岸后后,再修建地下電纜接入原電纜供電,試求該方案總施工費用的最小值;
處修建最短水下電纜到達對岸后后,再修建地下電纜接入原電纜供電,試求該方案總施工費用的最小值;
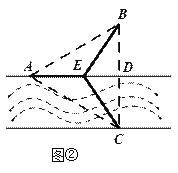
(2) 如圖②,點![]() 在線段
在線段![]() 上,且鋪設電纜的線路為
上,且鋪設電纜的線路為![]() .若
.若![]() ,試用
,試用![]() 表示出總施工費用
表示出總施工費用![]() (萬元)的解析式,并求
(萬元)的解析式,并求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com