
【題目】已知函數![]() ,
,![]() ,其中a為常數,e是自然對數的底數,曲線
,其中a為常數,e是自然對數的底數,曲線![]() 在其與y軸的交點處的切線記作
在其與y軸的交點處的切線記作![]() ,曲線
,曲線![]() 在其與x軸的交點處的切線記作
在其與x軸的交點處的切線記作![]() ,且
,且![]() .
.
(1)求![]() 之間的距離;
之間的距離;
(2)若存在x使不等式![]() 成立,求實數m的取值范圍.
成立,求實數m的取值范圍.
科目:高中數學 來源: 題型:
【題目】某公司為了解廣告投入對銷售收益的影響,在若干地區各投入![]() 萬元廣告費用,并將各地的銷售收益繪制成頻率分布直方圖(如圖所示).由于工作人員操作失誤,橫軸的數據丟失,但可以確定橫軸是從
萬元廣告費用,并將各地的銷售收益繪制成頻率分布直方圖(如圖所示).由于工作人員操作失誤,橫軸的數據丟失,但可以確定橫軸是從![]() 開始計數的. [附:回歸直線的斜率和截距的最小二乘估計公式分別為.]
開始計數的. [附:回歸直線的斜率和截距的最小二乘估計公式分別為.]
(1)根據頻率分布直方圖計算圖中各小長方形的寬度;
(2)試估計該公司投入![]() 萬元廣告費用之后,對應銷售收益的平均值(以各組的區間中點值代表該組的取值);
萬元廣告費用之后,對應銷售收益的平均值(以各組的區間中點值代表該組的取值);
(3)該公司按照類似的研究方法,測得另外一些數據,并整理得到下表:
廣告投入 | 1 | 2 | 3 | 4 | 5 |
銷售收益 | 2 | 3 | 2 | 7 |
由表中的數據顯示, ![]() 與
與![]() 之間存在著線性相關關系,請將(2)的結果填入空白欄,并求出
之間存在著線性相關關系,請將(2)的結果填入空白欄,并求出![]() 關于
關于![]() 的回歸直線方程.
的回歸直線方程.


查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了節能減排,發展低碳經濟,我國政府從2001年起就通過相關政策推動新能源汽車產業發展.下面的圖表反映了該產業發展的相關信息:
中國新能源汽車產銷情況一覽表 | ||||
新能源汽車生產情況 | 新能源汽車銷售情況 | |||
產品(萬輛) | 比上年同期 | 銷量(萬輛) | 比上年同期 | |
2018年3月 | 6.8 | 105 | 6.8 | 117.4 |
4月 | 8.1 | 117.7 | 8.2 | 138.4 |
5月 | 9.6 | 85.6 | 10.2 | 125.6 |
6月 | 8.6 | 31.7 | 8.4 | 42.9 |
7月 | 9 | 53.6 | 8.4 | 47.7 |
8月 | 9.9 | 39 | 10.1 | 49.5 |
9月 | 12.7 | 64.4 | 12.1 | 54.8 |
10月 | 14.6 | 58.1 | 13.8 | 51 |
11月 | 17.3 | 36.9 | 16.9 | 37.6 |
1-12月 | 127 | 59.9 | 125.6 | 61.7 |
2019年1月 | 9.1 | 113 | 9.6 | 138 |
2月 | 5.9 | 50.9 | 5.3 | 53.6 |
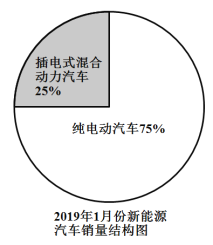
根據上述圖表信息,下列結論錯誤的是( )
A.2017年3月份我國新能源汽車的產量不超過![]() 萬輛
萬輛
B.2017年我國新能源汽車總銷量超過![]() 萬輛
萬輛
C.2018年8月份我國新能源汽車的銷量高于產量
D.2019年1月份我國插電式混合動力汽車的銷量低于![]() 萬輛
萬輛
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 四點都在拋物線
四點都在拋物線![]() 上.
上.
(1)若線段![]() 的斜率為
的斜率為![]() ,求線段
,求線段![]() 中點的縱坐標;
中點的縱坐標;
(2)記![]() ,若直線
,若直線![]() ,
,![]() 均過定點
均過定點![]() ,且
,且![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點,證明:
的中點,證明:![]() ,
,![]() ,
,![]() 三點共線.
三點共線.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 過點
過點![]() ,傾斜角為
,傾斜角為![]() ,在以坐標原點為極點,
,在以坐標原點為極點,![]() 軸的非負半軸為極軸的極坐標系中,曲線
軸的非負半軸為極軸的極坐標系中,曲線![]() 的方程為
的方程為![]() .
.
(1)寫出直線![]() 的參數方程和曲線
的參數方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點,設點
兩點,設點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】高鐵和航空的飛速發展不僅方便了人們的出行,更帶動了我國經濟的巨大發展.據統 計,在2018年這一年內從![]() 市到
市到![]() 市乘坐高鐵或飛機出行的成年人約為
市乘坐高鐵或飛機出行的成年人約為![]() 萬人次.為了 解乘客出行的滿意度,現從中隨機抽取
萬人次.為了 解乘客出行的滿意度,現從中隨機抽取![]() 人次作為樣本,得到下表(單位:人次):
人次作為樣本,得到下表(單位:人次):
滿意度 | 老年人 | 中年人 | 青年人 | |||
乘坐高鐵 | 乘坐飛機 | 乘坐高鐵 | 乘坐飛機 | 乘坐高鐵 | 乘坐飛機 | |
10分(滿意) | 12 | 1 | 20 | 2 | 20 | 1 |
5分(一般) | 2 | 3 | 6 | 2 | 4 | 9 |
0分(不滿意) | 1 | 0 | 6 | 3 | 4 | 4 |
(span>1)在樣本中任取![]() 個,求這個出行人恰好不是青年人的概率;
個,求這個出行人恰好不是青年人的概率;
(2)在2018年從![]() 市到
市到![]() 市乘坐高鐵的所有成年人中,隨機選取
市乘坐高鐵的所有成年人中,隨機選取![]() 人次,記其中老年人出行的人次為
人次,記其中老年人出行的人次為![]() .以頻率作為概率,求
.以頻率作為概率,求![]() 的分布列和數學期望;
的分布列和數學期望;
(3)如果甲將要從![]() 市出發到
市出發到![]() 市,那么根據表格中的數據,你建議甲是乘坐高鐵還是飛機? 并說明理由.
市,那么根據表格中的數據,你建議甲是乘坐高鐵還是飛機? 并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地要建造一個邊長為2(單位:![]() )的正方形市民休閑公園
)的正方形市民休閑公園![]() ,將其中的區域
,將其中的區域![]() 開挖成一個池塘,如圖建立平面直角坐標系后,點
開挖成一個池塘,如圖建立平面直角坐標系后,點![]() 的坐標為
的坐標為![]() ,曲線
,曲線![]() 是函數
是函數![]() 圖像的一部分,過邊
圖像的一部分,過邊![]() 上一點
上一點![]() 在區域
在區域![]() 內作一次函數
內作一次函數![]() (
(![]() )的圖像,與線段
)的圖像,與線段![]() 交于點
交于點![]() (點
(點![]() 不與點
不與點![]() 重合),且線段
重合),且線段![]() 與曲線
與曲線![]() 有且只有一個公共點
有且只有一個公共點![]() ,四邊形
,四邊形![]() 為綠化風景區.
為綠化風景區.
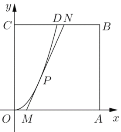
(1)求證:![]() ;
;
(2)設點![]() 的橫坐標為
的橫坐標為![]() ,
,
①用![]() 表示
表示![]() 、
、![]() 兩點的坐標;
兩點的坐標;
②將四邊形![]() 的面積
的面積![]() 表示成關于
表示成關于![]() 的函數
的函數![]() ,并求
,并求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線C的極坐標方程是ρ=6sinθ,建立以極點為坐標原點,極軸為x軸正半軸的平面直角坐標系.直線l的參數方程是![]() ,(t為參數).
,(t為參數).
(1)求曲線C的直角坐標方程;
(2)若直線l與曲線C相交于A,B兩點,且|AB|=![]() ,求直線的斜率k.
,求直線的斜率k.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com