
【題目】如圖1,在高為2的梯形ABCD中,AB∥CD,AB=2,CD=5,過A、B分別作AE⊥CD,BF⊥CD,垂足分別為E、F.已知DE=1,將梯形ABCD沿AE、BF同側折起,得空間幾何體ADE﹣BCF,如圖2. 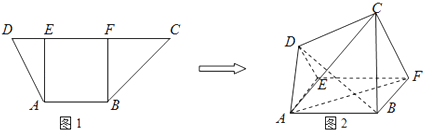
(Ⅰ)若AF⊥BD,證明:△BDE為直角三角形;
(Ⅱ)若DE∥CF, ![]() ,求平面ADC與平面ABFE所成角的余弦值.
,求平面ADC與平面ABFE所成角的余弦值.
【答案】解:證明:連接BE, 由已知可知四邊形ABFE是正方形,∴AF⊥BE,
又AF⊥BD,BE∩DE=E,
∴AF⊥平面BDE,又DE平面BDE,
∴AF⊥DE,
又DE⊥AE,AE∩AF=F,
∴DE⊥平面ABFE,又BE平面ABFE,
∴DE⊥BE,即△BDE為直角三角形.
(Ⅱ)取CF的中點M,連結DM,則四邊形DEFM是平行四邊形,
∴DM=EF=2,CM= ![]() CF=1,又CD=
CF=1,又CD= ![]() ,
,
∴cos∠CMD= ![]() =
= ![]() ,即∠CMD=∠CFE=60°,
,即∠CMD=∠CFE=60°,
過E作EG⊥EF,則EG⊥平面ABFE,
以E為原點,以EA,EF,EG為坐標軸建立空間直角坐標系,
則A(2,0,0),C(0,1, ![]() ),D(0,﹣
),D(0,﹣ ![]() ,
, ![]() ),
),
∴ ![]() =(﹣2,1,
=(﹣2,1, ![]() ),
), ![]() =(﹣2,﹣
=(﹣2,﹣ ![]() ,
, ![]() ),
),
設平面ACD的法向量為 ![]() =(x,y,z),則
=(x,y,z),則 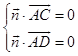 ,
,
即 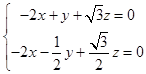 ,令z=
,令z= ![]() 得
得 ![]() =(1,﹣1,
=(1,﹣1, ![]() ),
),
又GE⊥平面ABFE,∴ ![]() =(0,0,1)是平面ABFE的一個法向量,
=(0,0,1)是平面ABFE的一個法向量,
∴cos< ![]() >=
>= ![]() =
= ![]() =
= ![]() ,
,
由圖形可知平面ADC與平面ABFE所成角為銳二面角,
∴平面ADC與平面ABFE所成角的余弦值為 ![]() .
.
【解析】(1)由AF⊥BE,AF⊥BD可得AF⊥平面BFE,得出AF⊥DE,結合DE⊥AE即可得出DE⊥平面ABFE,故而DE⊥BE;(2)求出∠CFE的大小,以E為原點建立空間坐標系,求出平面ACD和平面ABFE的法向量,計算兩法向量的夾角即可得出二面角的大小.
【考點精析】本題主要考查了直線與平面垂直的性質的相關知識點,需要掌握垂直于同一個平面的兩條直線平行才能正確解答此題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知![]() 是數列
是數列![]() 的前n項和,
的前n項和,![]() ,且
,且![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)對于正整數![]() ,已知
,已知![]() 成等差數列,求正整數
成等差數列,求正整數![]() 的值;
的值;
(3)設數列![]() 前n項和是
前n項和是![]() ,且滿足:對任意的正整數n,都有等式
,且滿足:對任意的正整數n,都有等式![]() 成立.求滿足等式
成立.求滿足等式![]() 的所有正整數n.
的所有正整數n.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一段時間內有2000輛車通過高速公路上的某處,現隨機抽取其中的200輛進行車速統計,統計結果如右面的頻率分布直方圖所示.若該處高速公路規定正常行駛速度為90km/h~120 km/h,試估計2000輛車中,在這段時間內以正常速度通過該處的汽車約有( )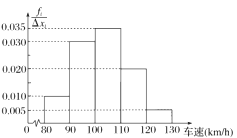
A.30輛
B.1700輛
C.170輛
D.300輛
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過拋物線 ![]() 的焦點,斜率為
的焦點,斜率為 ![]() 的直線交拋物線于
的直線交拋物線于 ![]() ,
, ![]() (
( ![]() )兩點,且
)兩點,且 ![]() .
.
(1)求該拋物線的方程;
(2)![]() 為坐標原點,
為坐標原點, ![]() 為拋物線上一點,若
為拋物線上一點,若 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某賽季,甲、乙兩名籃球運動員都參加了![]() 場比賽,比賽得分情況如下(單位:分)
場比賽,比賽得分情況如下(單位:分)
甲:![]()
乙:![]()

(1)根據得分情況記錄,作出兩名籃球運動員得分的莖葉圖,并根據莖葉圖,對甲、乙兩運動員得分作比較,寫出兩個統計結論;
(2)設甲籃球運動員![]() 場比賽得分平均值
場比賽得分平均值![]() ,將
,將![]() 場比賽得分
場比賽得分![]() 依次輸入如圖所示的程序框圖進行運算,問輸出的
依次輸入如圖所示的程序框圖進行運算,問輸出的![]() 大小為多少?并說明
大小為多少?并說明![]() 的統計學意義;
的統計學意義;
(3)如果從甲、乙兩位運動員的![]() 場得分中,各隨機抽取一場不少于
場得分中,各隨機抽取一場不少于![]() 分的得分,求甲的得分大于乙的得分的概率.
分的得分,求甲的得分大于乙的得分的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com