日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情
設a，b為實數，若復數
1+2i
a+bi
=i，則（　　）
分析：復數的方程兩邊同乘a+bi轉化復數的方程，利用復數相等，求出a，b的值，即可得到選項．
解答：解：由復數
1+2i
a+bi
=i可知1+2i=（a+bi）i=ai-b，
所以a=2，b=-1．
故選B．
點評：本題考查復數的乘除運算，復數的相等的充要條件的應用，考查計算能力．
練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

設復數β=x+yi（x，y∈R）與復平面上點P（x，y）對應．
（1）若β是關于t的一元二次方程t2-2t+m=0（m∈R）的一個虛根，且|β|=2，求實數m的值；
（2）設復數β滿足條件|β+3|+（-1）n|β-3|=3a+（-1）na（其中n∈N*、常數a∈ (
3
2
 ， 3)），當n為奇數時，動點P（x、y）的軌跡為C1．當n為偶數時，動點P（x、y）的軌跡為C2．且兩條曲線都經過點D(2，
2
)，求軌跡C1與C2的方程；
（3）在（2）的條件下，軌跡C2上存在點A，使點A與點B（x0，0）（x0＞0）的最小距離不小于
2
3
3
，求實數x0的取值范圍．

查看答案和解析>>

科目：高中數學 來源：2002年全國各省市高考模擬試題匯編 題型：013

有四個命題：

①若是實數，則正整數n的最小值是4

②設z是虛數，則z＋∈

③若都是非零復數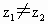，，且復平面上O為原點，點A和B分別與和對應，∠AOB＝，則

④若復數z滿足|z－|≤1，則≤arg(－zi)≤，其中真命題是

[　　]

A．①③④
B．①②③
C．①②④
D．②③④

查看答案和解析>>

科目：高中數學 來源：2013-2014學年福建省福州市高三上學期期末質量檢測理科數學試卷（解析版） 題型：選擇題

設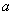是實數，若復數（i為虛數單位）在復平面內對應的點在直線x+y=0上，則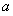的值為( )

A、－1 　　　B.0 　　　　　 C.1 　　　　 　　　D.2

 

查看答案和解析>>

科目：高中數學 來源：2010年上海市浦東新區高考數學二模試卷（文科）（解析版） 題型：解答題

設復數β=x+yi（x，y∈R）與復平面上點P（x，y）對應．
（1）若β是關于t的一元二次方程t2-2t+m=0（m∈R）的一個虛根，且|β|=2，求實數m的值；
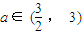（2）設復數β滿足條件|β+3|+（-1）n|β-3|=3a+（-1）na（其中n∈N*、常數），當n為奇數時，動點P（x、y）的軌跡為C1．當n為偶數時，動點P（x、y）的軌跡為C2．且兩條曲線都經過點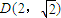，求軌跡C1與C2的方程；
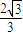（3）在（2）的條件下，軌跡C2上存在點A，使點A與點B（x，0）（x＞0）的最小距離不小于，求實數x的取值范圍．

查看答案和解析>>

科目：高中數學 來源：2010年上海市浦東新區高考數學二模試卷（理科）（解析版） 題型：解答題

設復數β=x+yi（x，y∈R）與復平面上點P（x，y）對應．
（1）若β是關于t的一元二次方程t2-2t+m=0（m∈R）的一個虛根，且|β|=2，求實數m的值；
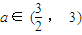（2）設復數β滿足條件|β+3|+（-1）n|β-3|=3a+（-1）na（其中n∈N*、常數），當n為奇數時，動點P（x、y）的軌跡為C1．當n為偶數時，動點P（x、y）的軌跡為C2．且兩條曲線都經過點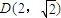，求軌跡C1與C2的方程；
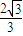（3）在（2）的條件下，軌跡C2上存在點A，使點A與點B（x，0）（x＞0）的最小距離不小于，求實數x的取值范圍．

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 久久国产亚洲 | aaa级片 | 亚洲精品久久久 | 日韩综合在线 | 国产激情毛片 | 欧美一区视频在线 | 国产精品视频一区二区三区不卡 | 成人av在线播放 | av网站有哪些 | 成人综合av| 成人性生交大片免费看中文带字幕 | 特级黄一级播放 | 日韩专区一区二区三区 | 欧美精品久久久久久久久老牛影院 | 国产精品一区二区三区在线播放 | 欧美一级在线 | 一区二区久久久 | 视频一区 中文字幕 | 色婷婷久久久久swag精品 | www.成人.com| 国产一区二区在线不卡 | 黄色免费一级 | 国产精品自产av一区二区三区 | 久久久女人 | 91精品国产高清一区二区性色 | 韩国精品视频在线观看 | 久久99影视| 黄色网址免费观看 | 一区二区中文字幕 | 精品国产乱码久久久久久88av | 久久综合一区二区三区 | 久久久九九 | 91麻豆产精品久久久久久 | 亚洲国产视频一区 | 国产欧美精品在线 | h视频免费 | hd国产人妖ts另类视频 | 日韩精品一二三区 | 国产精品看片 | 在线视频一区二区 | 午夜社区|