
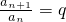 (常數),證明:{an}為非零常數列.
(常數),證明:{an}為非零常數列.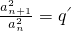 (常數),判斷{an}是否為非零常數列,并說明理由.
(常數),判斷{an}是否為非零常數列,并說明理由. ?qan-an=d?(q-1)an=d
?qan-an=d?(q-1)an=d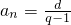 是一常數,矛盾,所以{an}為非零常數列; (5分)
是一常數,矛盾,所以{an}為非零常數列; (5分)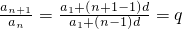 ,
, ,解得
,解得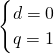 .由此可知數列{an}為非零常數列; (5分)
.由此可知數列{an}為非零常數列; (5分)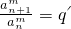 (常數),則當m為奇數時,{an}必為非零常數列;當m為偶數時,{an}不一定為非零常數列.
(常數),則當m為奇數時,{an}必為非零常數列;當m為偶數時,{an}不一定為非零常數列.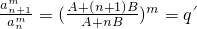 ,即
,即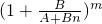 對一切n∈N*均為常數,則必有B=0,即有anm=A,當m為奇數時,
對一切n∈N*均為常數,則必有B=0,即有anm=A,當m為奇數時,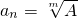 ,當m為偶數時,
,當m為偶數時,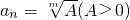 或者
或者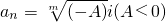 .3°{an}滿足an+1m-anm=d'(常數)且
.3°{an}滿足an+1m-anm=d'(常數)且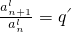 (常數),且m、l為整數,
(常數),且m、l為整數,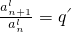 (正常數)可以轉化為
(正常數)可以轉化為 (常數),整個問題轉化為2°,結論顯然成立.(結論5分)
(常數),整個問題轉化為2°,結論顯然成立.(結論5分)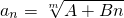 ,則
,則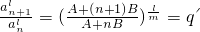 ,即
,即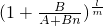 對一切n∈N*均為常數,則必有B=0,即有anm=A,則
對一切n∈N*均為常數,則必有B=0,即有anm=A,則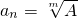 ,當m為偶數時,如反例:an=(-1)nn∈N*,它既滿足m次方后是等差數列,又是l(不管l為奇數還是偶數)次方后成等比數列,但它不為常數列.4°{an}滿足an+1m-anm=d'(常數)且
,當m為偶數時,如反例:an=(-1)nn∈N*,它既滿足m次方后是等差數列,又是l(不管l為奇數還是偶數)次方后成等比數列,但它不為常數列.4°{an}滿足an+1m-anm=d'(常數)且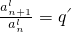 (常數),m、l為有理數,q′>0,則{an}必為非零常數列;否則{an}不一定為常數列.
(常數),m、l為有理數,q′>0,則{an}必為非零常數列;否則{an}不一定為常數列.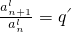 (常數),且m、l為實數,q′>0,{an}是不等于1的正數數列,則{an}必為非零且不等于1的常數列;否則{an}不一定為常數列.
(常數),且m、l為實數,q′>0,{an}是不等于1的正數數列,則{an}必為非零且不等于1的常數列;否則{an}不一定為常數列.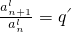 同樣可以轉化為
同樣可以轉化為 ,記anm=bn,由第(1)題的結論知:{bn}必為不等于1的正常數數列,也即{anm}為不等于1的正常數數列,
,記anm=bn,由第(1)題的結論知:{bn}必為不等于1的正常數數列,也即{anm}為不等于1的正常數數列,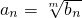 ,從而{an}也是不等于1的正常數數列.
,從而{an}也是不等于1的正常數數列.

科目:高中數學 來源: 題型:
| an+1 |
| an |
| ||
|
查看答案和解析>>
科目:高中數學 來源:閔行區二模 題型:解答題
| an+1 |
| an |
| ||
|
查看答案和解析>>
科目:高中數學 來源:2009年上海市閔行區高考數學一模試卷(文理合卷)(解析版) 題型:解答題
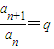 (常數),證明:{an}為非零常數列.
(常數),證明:{an}為非零常數列.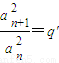 (常數),判斷{an}是否為非零常數列,并說明理由.
(常數),判斷{an}是否為非零常數列,并說明理由.查看答案和解析>>
科目:高中數學 來源:2009年上海市閔行區高考數學二模試卷(文理合卷)(解析版) 題型:解答題
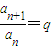 (常數),證明:{an}為非零常數列.
(常數),證明:{an}為非零常數列.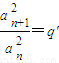 (常數),判斷{an}是否為非零常數列,并說明理由.
(常數),判斷{an}是否為非零常數列,并說明理由.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com