
過原點的直線交雙曲線  于P,Q兩點,現將坐標平面沿直線y= -x折成直二面角,則折后PQ長度的最小值等于
于P,Q兩點,現將坐標平面沿直線y= -x折成直二面角,則折后PQ長度的最小值等于
A. | B.4 | C. | D. |
B
解析試題分析:∵雙曲線 是等軸雙曲線,以直線y=±x為漸近線
是等軸雙曲線,以直線y=±x為漸近線
∴將雙曲線按逆時針方向旋轉45°角,可得雙曲線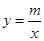 的圖象
的圖象
∵雙曲線 的頂點(
的頂點( ,0),逆時針方向旋轉45°
,0),逆時針方向旋轉45°
變為點( ,
, )
)
∴點( ,
, )在
)在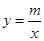 的圖象上,可得m=
的圖象上,可得m= ,
,
即雙曲線按逆時針方向旋轉45°角,得到雙曲線 的圖象
的圖象
問題轉化為:過原點的直線交雙曲線 于P、Q兩點
于P、Q兩點
將坐標平面沿直線y軸折成直二面角,求折后線段PQ的長度的最小值
設P(t, )(t>0),過點P作PM⊥y軸于M,連結MQ,
)(t>0),過點P作PM⊥y軸于M,連結MQ,
可得M(0, ),Q(-t,-
),Q(-t,- ),
),
|MQ|= =
= ,在折疊后的圖形中,Rt△PMQ中,|PM|=t,
,在折疊后的圖形中,Rt△PMQ中,|PM|=t,
得|PQ|2=|PM|2+|MQ|2= ≥
≥ =16,
=16,
當且僅當t2=4,即t=2時等號成立,
∴當t=2時,即P坐標為(2, )時,|PQ|的最小值為
)時,|PQ|的最小值為 =4.
=4.
綜上所述,折后線段PQ的長度的最小值等于4,故選B.
考點:兩點間的距離公式、面面垂直的性質、勾股定理,基本不等式求最值,邏輯推理能力,運算能力,轉化與化歸思想,數形結合思想


科目:高中數學 來源: 題型:解答題
已知圓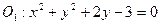 內一定點
內一定點 ,
, 為圓上的兩不同動點.
為圓上的兩不同動點.
(1)若 兩點關于過定點
兩點關于過定點 的直線
的直線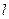 對稱,求直線
對稱,求直線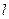 的方程.
的方程.
(2)若圓 的圓心
的圓心 與點
與點 關于直線
關于直線 對稱,圓
對稱,圓 與圓
與圓 交于
交于 兩點,且
兩點,且 ,求圓
,求圓 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
點P在正方體ABCD﹣A1B1C1D1的底面ABCD所在平面上,E是A1A的中點,且∠EPA=∠D1PD,則點P的軌跡是( )
| A.直線 | B.圓 | C.拋物線 | D.雙曲線 |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
已知拋物線的頂點在原點,焦點在x軸的正半軸上,若拋物線的準線與雙曲線5x2-y2= 20的兩條漸近線圍成的三角形的面積等于 ,則拋物線的方程為
,則拋物線的方程為
| A.y2=4x | B.y2=8x | C.x2=4y | D.x2=8y |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com