設函數f(x)=|x2-4x-5|.
(1)在區間[-2,6]上畫出函數f(x)的圖象;
(2)設集合A={x|f(x)≥5},B=(-∞,-2]∪[0,4]∪[6,+∞).試判斷集合A和B之間的關系(要寫出判斷過程);
(3)當k>2時,求證:在區間[-1,5]上,y=kx+3k的圖象位于函數f(x)圖象的上方.
分析:(1)當x2-4x-5>0時,f(x)=x2-4x-5;當x2-4x-5<0時,f(x)=x2-4x-5,進而畫出圖象.
(2)先求出f(x)≥5的解集,再判斷集合A和B的關系.
(3)設函數g(x)=kx+3k-f(x),只要證明g(x)>0恒成立即可.
解答:解:(1)設-2≤x≤6,當x
2-4x-5≥0時,
即6≥x≥5或-1≥x≥-2時,f(x)=x
2-4x-5=(x-2)
2-9
當x
2-4x-5<0時,即-1<x<5時,f(x)=-(x
2-4x-5)=-(x-2)
2+9
故作圖如下:
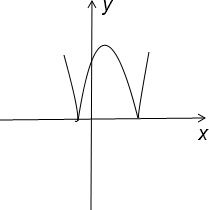
(2)方程f(x)=5的解分別是
2-,0,4和
2+,由于f(x)在(-∞,-1]和[2,5]上單調遞減,
在[-1,2]和[5,+∞)上單調遞增,
∴
A=( -∞, 2- ] ∪[ 0, 4 ]∪[ 2+, +∞ ).
由于2+
<6,2-
>-2
∴B?A.
(3)當x∈[-1,5]時,f(x)=-x
2+4x+5.
g(x)=k(x+3)-(-x
2+4x+5)=x
2+(k-4)x+(3k-5)=
(x-)2-,
∵k>2,∴
<1.又-1≤x≤5,
①當
-1≤<1,即2<k≤6時,
取
x=,g(x)
min=
-=-[(k-10)2-64].
∵16≤(k-10)
2<64,
∴(k-10)
2-64<0,則g(x)
min>0.
②當
<-1,即k>6時,取x=-1,g(x)
min=2k>0.
由①、②可知,當k>2時,g(x)>0,x∈[-1,5].
因此,在區間[-1,5]上,y=k(x+3)的圖象位于函數f(x)圖象的上方.
點評:本題主要考查了函數圖象的應用.注意數形結合.



