
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 為梯形,
為梯形, ![]() 底面
底面![]() ,
, ![]() .過
.過![]() 作一個平面
作一個平面![]() 使得
使得![]() 平面
平面![]() .
.
(1)求平面![]() 將四棱錐
將四棱錐![]() 分成兩部分幾何體的體積之比;
分成兩部分幾何體的體積之比;
(2)若平面![]() 與平面
與平面![]() 之間的距離為
之間的距離為![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.

【答案】(1)![]() 或
或![]() .(2)
.(2)![]()
【解析】試題分析:(1)設平面![]() 與直線
與直線![]() 分別交于
分別交于![]() ,因為
,因為![]() 平面
平面![]() ,所以
,所以![]() ,可得
,可得![]() 分別是
分別是![]() 的中點,根據棱錐的體積公式可得
的中點,根據棱錐的體積公式可得![]() ,從而可得平面
,從而可得平面![]() 將四棱錐
將四棱錐![]() 分成兩部分幾何體的體積之比;(2)因為
分成兩部分幾何體的體積之比;(2)因為![]() 兩兩垂直,以
兩兩垂直,以![]() 為
為![]() 軸,
軸, ![]() 軸,
軸, ![]() 軸建立空間直角坐標系,分別求出直線
軸建立空間直角坐標系,分別求出直線![]() 的方向向量以及平面
的方向向量以及平面![]() 的一個法向量,利用空間向量夾角余弦公式可得直線
的一個法向量,利用空間向量夾角余弦公式可得直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
試題解析:(1)記平面![]() 與直線
與直線![]() .
.
因為![]() ,所以
,所以![]() .
.
由已知條件易知![]() ,又因
,又因![]() .
.
所以![]()
可得![]()
所以![]() .
.
即平面![]() 將四棱錐
將四棱錐![]() 分成兩部分幾何體的體積之比為
分成兩部分幾何體的體積之比為![]() .
.
(2)建立直角坐標系,記![]()
則![]()
因為平面![]() 的法向量
的法向量![]()
![]()
設![]()
![]() 得
得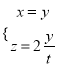 ,
,
取![]() 得平面
得平面![]() .
.
由條件易知點![]() 到平面
到平面![]() 距離
距離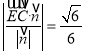 .即
.即![]() .
.
所以![]() .直線
.直線![]() 與平面
與平面![]() 所成角
所成角![]() 滿足
滿足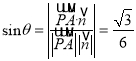
【方法點晴】本題主要考查棱錐的體積公式以及利用空間向量線面角,屬于難題.空間向量解答立體幾何問題的一般步驟是:(1)觀察圖形,建立恰當的空間直角坐標系;(2)寫出相應點的坐標,求出相應直線的方向向量;(3)設出相應平面的法向量,利用兩直線垂直數量積為零列出方程組求出法向量;(4)將空間位置關系轉化為向量關系;(5)根據定理結論求出相應的角和距離.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
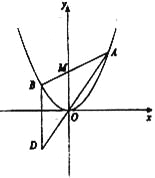
【題目】如圖所示,已知拋物線![]() ,過點
,過點![]() 任作一直線與
任作一直線與![]() 相交于
相交于![]() 兩點,過點
兩點,過點![]() 作
作![]() 軸的平行線與直線
軸的平行線與直線![]() 相交于點
相交于點![]() 為坐標原點).
為坐標原點).
(1)證明: 動點![]() 在定直線上;
在定直線上;
(2)作![]() 的任意一條切線
的任意一條切線![]() (不含
(不含![]() 軸), 與直線
軸), 與直線![]() 相交于點
相交于點![]() 與(1)中的定直線相交于點
與(1)中的定直線相交于點![]() .
.
證明: ![]() 為定值, 并求此定值.
為定值, 并求此定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線G:x2=2py(p>0),直線y=k(x﹣1)+2與拋物線G相交A(x1 , y1),B(x2 , y2)(x1<x2),過A,B點分別作拋物線G的切線L1 , L2 , 兩切線L1 , L2相交H(x,y),
(1)若k=1,有 L1⊥L2 , 求拋物線G的方程;
(2)若p=2,△ABH的面積為S1 , 直線AB與拋物線G圍成封閉圖形的面積為S2 , 證明: ![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學從參加環保知識竟賽的學生中抽取了部分學生的成績進行分析,不過作好的莖葉圖和頻率分布直方圖因故均受到不同程度的損壞,其可見部分信息如圖所示,據此解答下列問題:

(1)求抽取學生成績的中位數,并修復頻率分布直方圖;
(2)根據修復的頻率分布直方圖估計該中學此次環保知識競賽的平均成績。(以各組的區間中點值代表該組的各個值)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某玩具生產公司每天計劃生產衛兵、騎兵、傘兵這三種玩具共![]() 個,生產一個衛兵需
個,生產一個衛兵需![]() 分鐘,生產一個騎兵需
分鐘,生產一個騎兵需![]() 分鐘,生產一個傘兵需
分鐘,生產一個傘兵需![]() 分鐘,已知總生產時間不超過
分鐘,已知總生產時間不超過![]() 小時,若生產一個衛兵可獲利潤
小時,若生產一個衛兵可獲利潤![]() 元,生產一個騎兵可獲利潤
元,生產一個騎兵可獲利潤![]() 元,生產一個傘兵可獲利潤
元,生產一個傘兵可獲利潤![]() 元.
元.
(1)用每天生產的衛兵個數![]() 與騎兵個數
與騎兵個數![]() 表示每天的利潤
表示每天的利潤![]() (元);
(元);
(2)怎么分配生產任務才能使每天的利潤最大,最大利潤是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以下四個命題中,正確命題的個數是( )
①命題“若x=y,則sinx=siny”的逆否命題是真命題;
②已知α,β是不同的平面,m,n是不同的直線,m∥α,n∥β,α⊥β,則m⊥n;
③直線l1:2ax+y+1=0,l2:x+2ay+2=0,l1∥l2的充要條件是 ![]() ;
;
④ ![]() .
.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
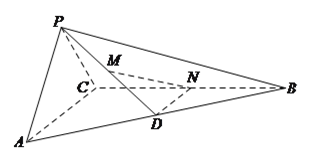
【題目】在三棱錐![]() 中,平面
中,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 為
為![]() 的中點,
的中點, ![]() 為
為![]() 的中點,
的中點, ![]() 在棱
在棱![]() 上.
上.
(![]() )當
)當![]() 為
為![]() 的中點時,證明:
的中點時,證明: ![]() 平面
平面![]() .
.
(![]() )求證:
)求證: ![]() 平面
平面![]() .
.
(![]() )是否存在點
)是否存在點![]() 使得
使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,說明理由.
的值,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】明天小強要參加班里組織的郊游活動,為了做好參加這次郊游的準備工作,他測算了如下數據:整理床鋪、收拾攜帶物品8分鐘,洗臉、刷牙7分鐘,煮牛奶15分鐘,吃早飯10分鐘,查公交線路圖9分鐘,給出差在外的父親發手機短信6分鐘,走到公共汽車站10分鐘,等公共汽車10分鐘.小強粗略地算了一下,總共需要75分鐘,為了趕上7:50的公共汽車,小強決定6:30起床,不幸的是他一下子睡到6:50,請你幫小強安排一下時間,畫出一份郊游出行前時間安排流程圖,使他還能來得及參加此次郊游.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com