
(本小題滿分12分)已知直三棱柱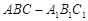 中,△
中,△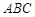 為等腰直角三角形,∠
為等腰直角三角形,∠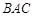 =
=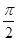 ,且
,且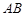 =
=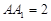 ,
,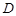 、
、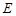 、
、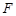 分別為
分別為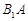 、
、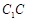 、
、 的中點.
的中點.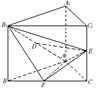
(1)求證: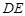 ∥平面
∥平面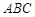 ;
;
(2)求證: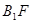 ⊥平面
⊥平面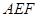 ;
;
(3)求三棱錐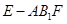 的體積.
的體積.
(1)設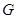 是
是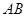 的中點,連結
的中點,連結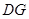 ,則
,則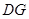 平行且等于
平行且等于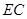 ,所以四邊形
,所以四邊形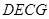 是平行四邊形,所以
是平行四邊形,所以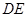 //
//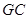 ,從而
,從而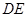 ∥平面
∥平面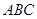 .
.
(2)∵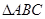 為等腰直角三角形,
為等腰直角三角形,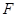 為
為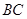 的中點,∴
的中點,∴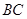 ⊥
⊥ ,又∵
,又∵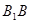 ⊥平面
⊥平面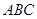 ,可證
,可證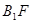 ⊥
⊥ ∵
∵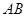 =
=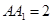 ,∴
,∴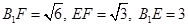 ,∴
,∴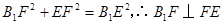 ,∵
,∵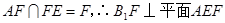
(3)1
解析試題分析:(1)方法1:設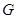 是
是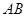 的中點,連結
的中點,連結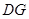 ,則
,則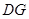 平行且等于
平行且等于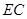 ,…(2分)
,…(2分)
所以四邊形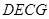 是平行四邊形,所以
是平行四邊形,所以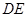 //
//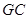 ,
,
從而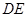 ∥平面
∥平面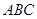 . …………(4分)
. …………(4分)
方法2:連接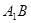 、
、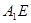 ,并延長
,并延長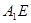 交
交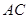 的延長線于點
的延長線于點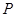 ,連接
,連接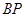 .
.
由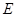 為
為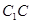 的中點,
的中點,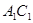 ‖
‖ ,可證
,可證 ……(2分)
……(2分)
∵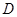 、
、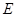 是
是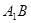 、
、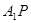 的中點,∴
的中點,∴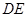 ‖
‖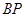 ,又∵
,又∵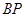
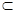 平面
平面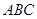 ,
,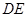
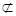 平面
平面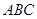 ,∴
,∴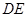 ∥平面
∥平面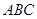 ………(4分)
………(4分)
(2)∵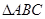 為等腰直角三角形,
為等腰直角三角形,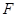 為
為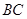 的中點,∴
的中點,∴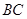 ⊥
⊥ ,
,
又∵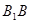 ⊥平面
⊥平面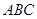 ,可證
,可證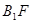 ⊥
⊥ ……(6分)
……(6分)
∵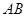 =
=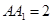 ,∴
,∴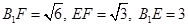 ,
,
∴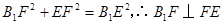 ,
,
∵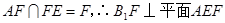 ……(8分)
……(8分)
(3)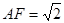 ,
,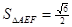 ,…………(10分)
,…………(10分)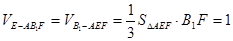 …………(12分)
…………(12分)
考點:本題考查了空間中的線面關系及體積的求解
點評:高考中常考查空間中平行關系與垂直關系的證明以及幾何體體積的計算,這是高考的重點內容.證明的關鍵是熟練掌握并靈活運用相關的判定定理與性質定理.


科目:高中數學 來源: 題型:解答題
如圖,四邊形 中,
中, 為正三角形,
為正三角形, ,
,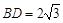 ,
, 與
與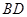 交于
交于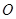 點.將
點.將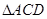 沿邊
沿邊 折起,使
折起,使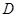 點至
點至 點,已知
點,已知 與平面
與平面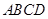 所成的角為
所成的角為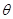 ,且
,且 點在平面
點在平面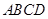 內的射影落在
內的射影落在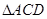 內.
內.
(Ⅰ)求證: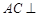 平面
平面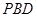 ;
;
(Ⅱ)若已知二面角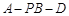 的余弦值為
的余弦值為 ,求
,求 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖所示在四棱錐P—ABCD中,平面PAB⊥平面ABCD,底面ABCD是邊長為2的正方形,△PAB為等邊三角形。(12分)
(1)求PC和平面ABCD所成角的大小;
(2)求二面角B─AC─P的大小。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
已知如圖(1),正三角形ABC的邊長為2a,CD是AB邊上的高,E、F分別是AC和BC邊上的點,且滿足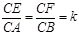 ,現將△ABC沿CD翻折成直二面角A-DC-B,如圖(2).
,現將△ABC沿CD翻折成直二面角A-DC-B,如圖(2). 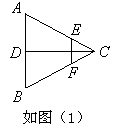
(Ⅰ) 求二面角B-AC-D的大小;
(Ⅱ) 若異面直線AB與DE所成角的余弦值為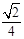 ,求k的值.
,求k的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(12分)如圖,在正方體ABCD-A1B1C1D1中,E、F、G分別是CB、CD、CC1的中點,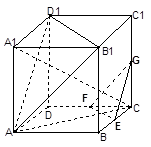
(1)求證:平面A B1D1∥平面EFG;
(2)求證:平面AA1C⊥面EFG.
(3)求異面直線AC與A1B所成的角
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
如圖,在三棱錐D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E為BC的中點,F在棱AC上,且AF=3FC.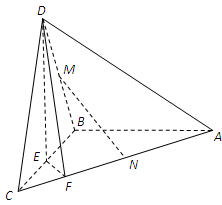
(1)求三棱錐D-ABC的表面積;
(2)求證AC⊥平面DEF;
(3)若M為BD的中點,問AC上是否存在一點N,使MN∥平面DEF?若存在,說明點N的位置;若不存在,試說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
在直三棱柱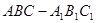 中, AC=4,CB=2,AA1=2,
中, AC=4,CB=2,AA1=2,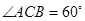 ,E、F分別是
,E、F分別是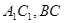 的中點。
的中點。
(1)證明:平面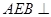 平面
平面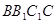 ;
;
(2)證明: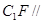 平面ABE;
平面ABE;
(3)設P是BE的中點,求三棱錐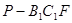 的體積。
的體積。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)如圖,矩形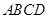 所在平面與平面
所在平面與平面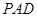 垂直,
垂直,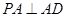 ,且
,且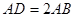 ,
,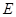 為
為 上的動點.
上的動點.
(Ⅰ)當 為
為 的中點時,求證:
的中點時,求證: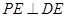 ;
;
(Ⅱ)若 ,在線段
,在線段 上是否存在點E,使得二面角
上是否存在點E,使得二面角 的大小為
的大小為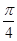 . 若存在,確定點E的位置,若不存在,說明理由.
. 若存在,確定點E的位置,若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com