【題目】如圖，第1個圖形由正三角形擴展而成，共12個頂點.第n個圖形是由正n+2邊形擴展而來 
，則第n+1個圖形的頂點個數是 ( )
（1） 
（2）
（3） 
（4）
A. (2n+1)(2n+2)B. 3(2n+2)C. (n+2)(n+3)D. (n+3)(n+4)
七彩題卡口算應用一點通系列答案科目：高中數學 來源： 題型：
【題目】從甲、乙兩名學生中選拔一人參加射擊比賽，對他們的射擊水平進行了測試，兩人在相同條件下各射擊10次，命中的環數如下：
甲：7，8，6，9，6，5，9，9，7，4.
乙：9，5，7，8，7，6，8，6，7，7.
（1）分別計算甲、乙兩人射擊命中環數的極差、眾數和中位數；
（2）分別計算甲、乙兩人射擊命中環數的平均數、方差、標準差；
（3）比較兩人的成績，然后決定選擇哪一個人參賽.
查看答案和解析>>
科目：高中數學 來源： 題型：
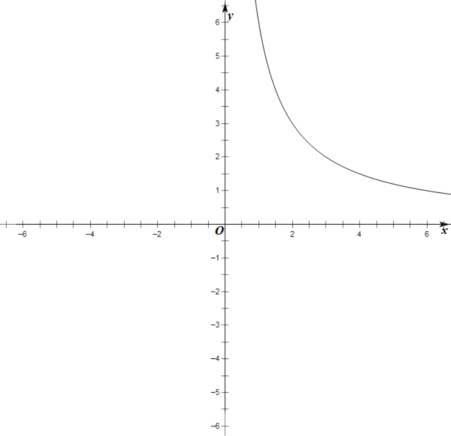
【題目】某班數學興趣小組對函數
的圖象和性質將進行了探究，探究過程如下，請補充完整．
（1）自變量
的取值范圍是除
外的全體實數，與
的幾組對應值列表如下：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中，
_________；
（2）根據上表數據，在如圖所示的平面直角坐標系中描點并畫出了函數圖象的一部分，請畫出該函數圖象的另一部分；
（3）觀察函數圖象，寫出一條函數性質；
（4）進一步探究函數圖象發現：
①函數圖象與軸交點情況是________，所以對應方程
的實數根的情況是________；
②方程
有_______個實數根；
③關于的方程
有
個實數根，
的取值范圍是________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】從
年
月份，某市街頭出現共享單車，到
月份，根據統計，市區所有人騎行過共享單車的人數已占
，騎行過共享單車的人數中，有
是大學生（含大中專及高職），該市區人口按
萬計算，大學生人數約
萬人.
（1）任選出一名大學生，求他（她）騎行過共享單車的概率；
（2）隨單車投放數量增加，亂停亂放成為城市管理的問題，以下是累計投放單車數量
與亂停亂放單車數量
之間的關系圖表：
累計投放單車數量 |
|
|
|
|
|
亂停亂放單車數量 |
|
|
|
|
|
①計算
關于
的線性回歸方程（其中
精確到
值保留三位有效數字），并預測當
時，單車亂停亂放的數量；
②已知該市共有五個區，其中有兩個區的單車亂停亂放數量超過標準.在“雙創”活動中，檢查組隨機抽取三個區調查單車亂停亂放數量， 
表示“單車亂停亂放數量超過標準的區的個數”，求
的分布列和數學期望
.
參考公式和數據：回歸直線方程
中的斜率和截距的最小二乘法估計公式分別為
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】有一容量為50的樣本,數據的分組以及各組的頻數如下:
[12.5,15.5),3;[15.5,18.5),8;[18.5,21.5),9;[21.5,24.5),11;[24.5,27.5),10;[27.5,30.5),5;[30.5,33.5],4.
(1)列出樣本的頻率分布表.
(2)畫出頻率分布直方圖.
(3)根據頻率分布表,估計數據落在[15.5,24.5)內的可能性約是多少?
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了解某班學生喜愛打籃球是否與性別有關，對本班50人進行了問卷調查得到了如下的列聯表：
喜愛打籃球 | 不喜愛打籃球 | 合計 | |
男生 | 5 | ||
女生 | 10 | ||
合計 | ５０ |
已知在全部50人中隨機抽取1人抽到喜愛打籃球的學生的概率為
．
（1）請將上面的列聯表補充完整；
（2）是否在犯錯誤的概率不超過0.5%的前提下認為喜愛打籃球與性別有關？說明你的理由.下面的臨界值表供參考：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005] | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式：
，其中
)
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】[選修4－4：坐標系與參數方程]
在直角坐標系
中，曲線
的參數方程為
（
為參數），直線
的參數方程為
（
為參數）.
（1）求和的直角坐標方程；
（2）若曲線截直線所得線段的中點坐標為
，求的斜率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
