
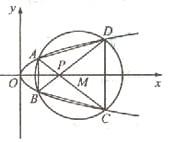
 如圖,已知拋物線
如圖,已知拋物線![]()
![]() 與圓
與圓![]() 相交于A、B、C、D四個(gè)點(diǎn)。
相交于A、B、C、D四個(gè)點(diǎn)。
(Ⅰ)求r的取值范圍
(Ⅱ)當(dāng)四邊形ABCD的面積最大時(shí),求對角線AC、BD的交點(diǎn)P的坐標(biāo)。
(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
(Ⅰ)將拋物線![]() 代入圓
代入圓![]() 的方程,消去
的方程,消去![]() ,整理得
,整理得![]() .............(1)
.............(1)
拋物線![]() 與圓
與圓![]() 相交于
相交于![]() 、
、![]() 、
、![]() 、
、![]() 四個(gè)點(diǎn)的充要條件是:方程(1)有兩個(gè)不相等的正根
四個(gè)點(diǎn)的充要條件是:方程(1)有兩個(gè)不相等的正根
∴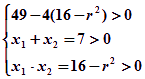 即
即 。解這個(gè)方程組得
。解這個(gè)方程組得![]()
![]() .
.
(II) 設(shè)四個(gè)交點(diǎn)的坐標(biāo)分別為![]() 、
、![]() 、
、![]() 、
、![]() 。
。
則由(I)根據(jù)韋達(dá)定理有![]() ,
,![]()
則![]()
![]()
令![]() ,則
,則![]() 下面求
下面求![]() 的最大值。
的最大值。
方法1:由三次均值有:
![]()
![]()
當(dāng)且僅當(dāng)![]() ,即
,即![]() 時(shí)取最大值。經(jīng)檢驗(yàn)此時(shí)
時(shí)取最大值。經(jīng)檢驗(yàn)此時(shí)![]() 滿足題意。
滿足題意。
法2:設(shè)四個(gè)交點(diǎn)的坐標(biāo)分別為![]() 、
、![]() 、
、![]() 、
、![]()
則直線AC、BD的方程分別為
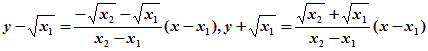
解得點(diǎn)P的坐標(biāo)為![]() 。
。
設(shè)![]() ,由
,由![]() 及(Ⅰ)得
及(Ⅰ)得![]()
![]()
由于四邊形ABCD為等腰梯形,因而其面積![]()
則![]() 將
將![]() ,
,![]() 代入上式,并令
代入上式,并令![]() ,等
,等
![]() ,
,
∴![]() ,
,
令![]() 得
得![]() ,或
,或![]() (舍去)
(舍去)
當(dāng)![]() 時(shí),
時(shí),![]() ;當(dāng)
;當(dāng)![]() 時(shí)
時(shí)![]() ;當(dāng)
;當(dāng)![]() 時(shí),
時(shí),![]()
故當(dāng)且僅當(dāng)![]() 時(shí),
時(shí),![]() 有最大值,即四邊形ABCD的面積最大,故所求的點(diǎn)P的坐標(biāo)為
有最大值,即四邊形ABCD的面積最大,故所求的點(diǎn)P的坐標(biāo)為![]() 。
。 ![]()



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
 如圖,已知拋物線
如圖,已知拋物線![]()
![]() 與圓
與圓![]() 相交于A、B、C、D四個(gè)點(diǎn)。
相交于A、B、C、D四個(gè)點(diǎn)。
(Ⅰ)求r的取值范圍
(Ⅱ)當(dāng)四邊形ABCD的面積最大時(shí),求對角線AC、BD的交點(diǎn)P的坐標(biāo)。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
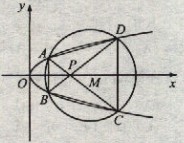
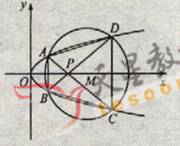 (22) (本小題滿分12分)(注意:在試題卷上作答無效)如圖,已知拋物線
(22) (本小題滿分12分)(注意:在試題卷上作答無效)如圖,已知拋物線![]()
![]() 與圓
與圓![]() 相交于A、B、C、D四個(gè)點(diǎn)。
相交于A、B、C、D四個(gè)點(diǎn)。
(Ⅰ)求r的取值范圍
(Ⅱ)當(dāng)四邊形ABCD的面積最大時(shí),求對角線AC、BD的交點(diǎn)P的坐標(biāo)。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010屆高三數(shù)學(xué)每周精析精練:圓錐曲線 題型:解答題
(注意:在試題卷上作答無效)
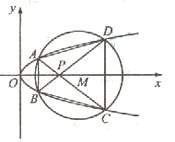 如圖,已知拋物線
如圖,已知拋物線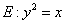
 與圓
與圓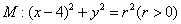 相交于A、B、C、D四個(gè)點(diǎn)。
相交于A、B、C、D四個(gè)點(diǎn)。
(Ⅰ)求r的取值范圍
(Ⅱ)當(dāng)四邊形ABCD的面積最大時(shí),求對角線AC、BD的交點(diǎn)P的坐標(biāo)。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010年陜西省西安市鐵一中高二下學(xué)期期中考試數(shù)學(xué)(文) 題型:解答題
(附加題)本題滿分20分
如圖,已知拋物線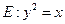
 與圓
與圓 相交于A、B、C、D四個(gè)點(diǎn)。
相交于A、B、C、D四個(gè)點(diǎn)。
(Ⅰ)求r的取值范圍 (Ⅱ)當(dāng)四邊形ABCD的面積最大時(shí),求對角線AC、BD的交點(diǎn)P的坐標(biāo)。
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com