
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為矩形,
為矩形,![]() 是等邊三角形,
是等邊三角形,![]() 是直角三角形,
是直角三角形,![]() 為
為![]() 中點.
中點.
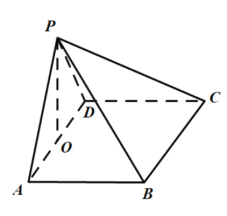
(1)求證:![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)證明見解析 (2)![]()
【解析】
(1)取![]() 的中點
的中點![]() ,根據等邊三角形性質得
,根據等邊三角形性質得![]() ,根據矩形性質得
,根據矩形性質得![]() ,最好根據線面垂直判定定理與性質定理得結果;
,最好根據線面垂直判定定理與性質定理得結果;
(2)法一:建立空間直角坐標系,利用向量數量積求各面方向量 ,再根據二面角與法向量夾角關系求結果;法二:取![]() 的中點
的中點![]() ,證明
,證明![]() 為二面角
為二面角![]() 的平面角,再根據解三角形得結果.
的平面角,再根據解三角形得結果.
(1)取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,
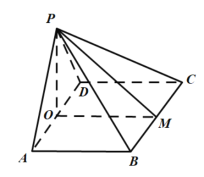
在等邊三角形![]() 中,
中,![]() ;
;
在矩形![]() 中,
中,![]() ,則
,則![]() .
.
∵![]() ,∴
,∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
(2)法一:設![]() ,則
,則![]() ,
,
∵![]() 且點
且點![]() 為
為![]() 的中點,(三線合一)
的中點,(三線合一)
∴![]() 為等腰直角三角形且
為等腰直角三角形且![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() 兩兩垂直
兩兩垂直
以![]() 為原點,
為原點,![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,
軸,
建立空間直角坐標系,
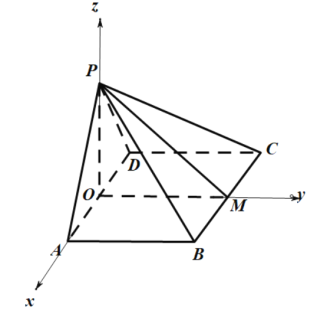
則![]() ,
,
![]() .
.
設平面![]() 的一個法向量為的
的一個法向量為的![]() ,由
,由 得
得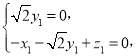
令![]() 得
得![]() .
.
(注:也可證明![]() 為平面
為平面![]() 的一個法向量)
的一個法向量)
設平面![]() 的一個法向量為
的一個法向量為![]() ,由
,由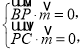 得
得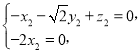
令![]() 得
得![]() .
.
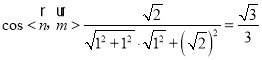 .
.
由圖知,二面角![]() 為鈍角,則二面角
為鈍角,則二面角![]() 的余弦值為
的余弦值為![]() .
.
(2)法二:
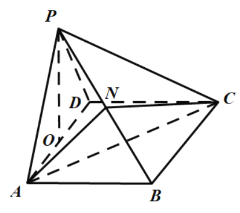
設![]() ,則
,則![]() ,
,
∵![]() 且點
且點![]() 為
為![]() 的中點,(三線合一)
的中點,(三線合一)
∴![]() 為等腰直角三角形,∴
為等腰直角三角形,∴![]() ,
,
∴![]() 為等腰三角形,
為等腰三角形,
取![]() 的中點
的中點![]() ,連接
,連接![]() ,∵
,∵![]() ,∴
,∴![]() .
.
在等邊三角形![]() 中,連接
中,連接![]() ,則
,則![]() ,
,![]() .
.
則![]() 為二面角
為二面角![]() 的平面角.
的平面角.
連接![]() ,在
,在![]() 中,由余弦定理,
中,由余弦定理,![]() .
.
則二面角![]() 的余弦值為
的余弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,某人打算做一個正四棱錐形的金字塔模型,先用木料搭邊框,再用其他材料填充,已知金字塔的每一條棱和邊都相等.
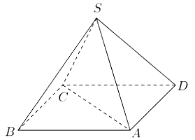
(1)求證:直線AC垂直于直線SD;
(2)若搭邊框共使用木料24米,則需要多少立方米的填充材料才能將整個金字塔內部填滿?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動點![]() 到點
到點![]() 的距離與它到直線
的距離與它到直線![]() 的距離
的距離![]() 的比值為
的比值為![]() ,設動點
,設動點![]() 形成的軌跡為曲線
形成的軌跡為曲線![]() ..
..
(1)求曲線![]() 的方程;
的方程;
(2)過點![]() 的直線與曲線
的直線與曲線![]() 交于
交于![]() 兩點,過
兩點,過![]() 點作
點作![]() ,垂足為
,垂足為![]() ,過
,過![]() 點作
點作![]() ,垂足為
,垂足為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若數列![]() 中存在三項,按一定次序排列構成等比數列,則稱
中存在三項,按一定次序排列構成等比數列,則稱![]() 為“等比源數列”。
為“等比源數列”。
(1)在無窮數列![]() 中,
中,![]() ,
,![]() ,求數列
,求數列![]() 的通項公式;
的通項公式;
(2)在(1)的結論下,試判斷數列![]() 是否為“等比源數列”,并證明你的結論;
是否為“等比源數列”,并證明你的結論;
(3)已知無窮數列![]() 為等差數列,且
為等差數列,且![]() ,
,![]() (
(![]() ),求證:數列
),求證:數列![]() 為“等比源數列”.
為“等比源數列”.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列 ![]() 的前
的前![]() 項和為
項和為![]() ,對一切
,對一切![]() ,點
,點![]() 都在函數
都在函數![]() 的圖象上.
的圖象上.
(1)求![]() ,歸納數列
,歸納數列![]() 的通項公式(不必證明);
的通項公式(不必證明);
(2)將數列![]() 依次按1項、2項、3項、4項循環地分為
依次按1項、2項、3項、4項循環地分為![]() ,
,![]() ,
,![]() ,
, ![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,…,分別計算各個括號內各數之和,設由這些和按原來括號的前后順序構成的數列為
,…,分別計算各個括號內各數之和,設由這些和按原來括號的前后順序構成的數列為![]() ,求
,求![]() 的值;
的值;
(3)設![]() 為數列
為數列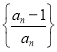 的前
的前![]() 項積,若不等式
項積,若不等式![]() 對一切
對一切![]() 都成立,其中
都成立,其中![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的中心為
的中心為![]() ,一個方向向量為
,一個方向向量為![]() 的直線
的直線![]() 與
與![]() 只有一個公共點
只有一個公共點![]()
(1)若![]() 且點
且點![]() 在第二象限,求點
在第二象限,求點![]() 的坐標;
的坐標;
(2)若經過![]() 的直線
的直線![]() 與
與![]() 垂直,求證:點
垂直,求證:點![]() 到直線
到直線![]() 的距離
的距離![]() ;
;
(3)若點![]() 、
、![]() 在橢圓上,記直線
在橢圓上,記直線![]() 的斜率為
的斜率為![]() ,且
,且![]() 為直線
為直線![]() 的一個法向量,且
的一個法向量,且![]() 求
求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業在“精準扶貧”行動中,決定幫助一貧困山區將水果運出銷售.現有8輛甲型車和4輛乙型車,甲型車每次最多能運6噸且每天能運4次,乙型車每次最多能運10噸且每天能運3次,甲型車每天費用320元,乙型車每天費用504元.若需要一天內把180噸水果運輸到火車站,則通過合理調配車輛運送這批水果的費用最少為______元.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】自然狀態下的魚類是一種可再生資源,為了持續利用這一資源,需從宏觀上考察其再生能力及捕撈強度對魚群總量的影響.用![]() 表示某魚群在第
表示某魚群在第![]() 年年初的總量且
年年初的總量且![]() .不考慮其他因素,設在第
.不考慮其他因素,設在第![]() 年內魚群的繁殖量及捕撈量都與
年內魚群的繁殖量及捕撈量都與![]() 成正比,死亡量與
成正比,死亡量與![]() 成正比,這些比例系數依次為正常數
成正比,這些比例系數依次為正常數![]() ,
,![]() ,
,![]()
(1)求![]() 與
與![]() 的關系式
的關系式
(2)若每年年初魚群的總量保持不變,求![]() ,
,![]() ,
,![]() ,
,![]() 所應滿足的條件
所應滿足的條件
(3)設![]() ,
,![]() ,為保證對任意
,為保證對任意![]() ,都有
,都有![]() ,則捕撈強度
,則捕撈強度![]() 的最大允許值是多少?并說明理由.
的最大允許值是多少?并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com