
【題目】某企業有甲、乙兩套設備生產同一種產品,為了檢測兩套設備的生產質量情況,隨機從兩套設備生產的大量產品中各隨機抽取了100件產品作為樣本來檢測一項質量指標值,若產品的該項質量指標值落在![]() 內,則為合格品,否則為不合格品.表1是甲套設備的樣本的頻數分布表,圖是乙套設備的樣本的頻率分布直方圖.
內,則為合格品,否則為不合格品.表1是甲套設備的樣本的頻數分布表,圖是乙套設備的樣本的頻率分布直方圖.

表甲套設備的樣本的頻數分布表
質量指標值 |
|
|
|
|
|
|
頻數 | 2 | 10 | 36 | 38 | 12 | 2 |
(1)將頻率視為概率.若乙套設備生產了10000件產品,則其中的合格品約有多少件?
(2)填寫下面的2×2列聯表,并判斷能否在犯錯誤的概率不超過0.01的前提下,認為該企業生產的這種產品的質量指標值與甲、乙兩套設備的選擇有關.
甲套設備 | 乙套設備 | 合計 | |
合格品 | |||
不合格品 | |||
合計 |
附表及公式: ,其中
,其中![]() ;
;
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【答案】(1)8600件;(2)列聯表見解析,不能在犯錯誤的概率不超過0.01的前提下可以認為該企業生產的這種產品的質量指標值與甲、乙兩套設備的選擇有關.
【解析】
(1)計算出不合格品率,和不合格品件數,由此求得合格品件數.(2)根據題目所給表格和圖像數據,填寫好![]() 聯表,計算出
聯表,計算出![]() 的值,由此判斷出“不能在犯錯誤的概率不超過0.01的前提下可以認為該企業生產的這種產品的質量指標值與甲、乙兩套設備的選擇有關.”
的值,由此判斷出“不能在犯錯誤的概率不超過0.01的前提下可以認為該企業生產的這種產品的質量指標值與甲、乙兩套設備的選擇有關.”
解:(1)由題圖1知,乙套設備生產的不合格品的概率約為![]() ,
,
∴乙套設備生產的10000件產品中不合格品約為![]() (件),
(件),
故合格品的件數為![]() (件).
(件).
(2)由題中的表1和圖1得到2×2列聯表如下:
甲套設備 | 乙套設備 | 合計 | |
合格品 | 96 | 86 | 182 |
不合格品 | 4 | 14 | 18 |
合計 | 100 | 100 | 200 |
將2×2列聯表中的數據代入公式計算得![]() 的觀測值
的觀測值![]() ,
,
因為6.105<6.635,
所以不能在犯錯誤的概率不超過0.01的前提下可以認為該企業生產的這種產品的質量指標值與甲、乙兩套設備的選擇有關.


科目:高中數學 來源: 題型:
【題目】設集合A={x|(x-3)(x+a)<0,a∈R},集合B={x∈Z|x2-3x-4<0}.
(1)若A∩B的子集個數為4,求a的范圍;
(2)若a∈Z,當A∩B≠![]() 時,求a的最小值,并求當a取最小值時A∪B.
時,求a的最小值,并求當a取最小值時A∪B.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,A,B是半徑為2的圓周上的定點,P為圓周上的動點,![]() 是銳角,大小為β.圖中陰影區域的面積的最大值為
是銳角,大小為β.圖中陰影區域的面積的最大值為
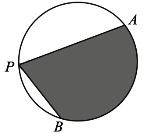
A. 4β+4cosβB. 4β+4sinβC. 2β+2cosβD. 2β+2sinβ
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】 如圖,在四棱錐![]() 中,底面
中,底面![]() 為平行四邊形,
為平行四邊形,![]() 為等邊三角形,平面
為等邊三角形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,

(Ⅰ)設![]() 分別為
分別為![]() 的中點,求證:
的中點,求證:![]() 平面
平面![]() ;
;
(Ⅱ)求證:![]() 平面
平面![]() ;
;
(Ⅲ)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】天津大學某學院欲安排4名畢業生到某外資企業的三個部門![]() 實習,要求每個部門至少安排1人,其中甲大學生不能安排到
實習,要求每個部門至少安排1人,其中甲大學生不能安排到![]() 部門工作的方法有_______種(用數字作答).
部門工作的方法有_______種(用數字作答).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【選修4-4:坐標系與參數方程】
在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為:
的參數方程為: ![]() (
(![]() 為參數,
為參數, ![]() ),將曲線
),將曲線![]() 經過伸縮變換:
經過伸縮變換:  得到曲線
得到曲線![]() .
.
(1)以原點為極點, ![]() 軸的正半軸為極軸建立坐標系,求
軸的正半軸為極軸建立坐標系,求![]() 的極坐標方程;
的極坐標方程;
(2)若直線![]() (
(![]() 為參數)與
為參數)與![]() 相交于
相交于![]() 兩點,且
兩點,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,側棱
中,側棱![]() 底面
底面![]() ,底面
,底面![]() 為長方形,且
為長方形,且![]() ,
,![]() 是
是![]() 的中點,作
的中點,作![]() 交
交![]() 于點
于點![]() .
.

(1)證明:![]() 平面
平面![]() ;
;
(2)若三棱錐![]() 的體積為
的體積為![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(3)在(2)的條件下,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】正三棱柱![]() (底面是正三角形,側棱垂直底面)的各條棱長均相等,
(底面是正三角形,側棱垂直底面)的各條棱長均相等,![]() 為
為![]() 的中點.
的中點.![]() 、
、![]() 分別是
分別是![]() 、
、![]() 上的動點(含端點),且滿足
上的動點(含端點),且滿足![]() .當
.當![]() 運動時,下列結論中正確的是______ (填上所有正確命題的序號).
運動時,下列結論中正確的是______ (填上所有正確命題的序號).

①平面![]() 平面
平面![]() ;
;
②三棱錐![]() 的體積為定值;
的體積為定值;
③![]() 可能為直角三角形;
可能為直角三角形;
④平面![]() 與平面
與平面![]() 所成的銳二面角范圍為
所成的銳二面角范圍為![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】分形幾何學是一門以不規則幾何形態為研究對象的幾何學.分形的外表結構極為復雜,但其內部卻是有規律可尋的.一個數學意義上分形的生成是基于一個不斷迭代的方程式,即一種基于遞歸的反饋系統.下面我們用分形的方法來得到一系列圖形,如圖1,線段![]() 的長度為a,在線段
的長度為a,在線段![]() 上取兩個點
上取兩個點![]() ,
,![]() ,使得
,使得![]() ,以
,以![]() 為一邊在線段
為一邊在線段![]() 的上方做一個正六邊形,然后去掉線段
的上方做一個正六邊形,然后去掉線段![]() ,得到圖2中的圖形;對圖2中的最上方的線段
,得到圖2中的圖形;對圖2中的最上方的線段![]() 作相同的操作,得到圖3中的圖形;依此類推,我們就得到了以下一系列圖形:
作相同的操作,得到圖3中的圖形;依此類推,我們就得到了以下一系列圖形:

記第![]() 個圖形(圖1為第1個圖形)中的所有線段長的和為
個圖形(圖1為第1個圖形)中的所有線段長的和為![]() ,現給出有關數列
,現給出有關數列![]() 的四個命題:
的四個命題:
①數列![]() 是等比數列;
是等比數列;
②數列![]() 是遞增數列;
是遞增數列;
③存在最小的正數![]() ,使得對任意的正整數
,使得對任意的正整數![]() ,都有
,都有![]() ;
;
④存在最大的正數![]() ,使得對任意的正整數
,使得對任意的正整數![]() ,都有
,都有![]() .
.
其中真命題的序號是________________(請寫出所有真命題的序號).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com