
【題目】下面的莖葉圖記錄了甲、乙兩代表隊各10名同學在一次英語聽力比賽中的成績(單位:分).已知甲代表隊數據的中位數為76,乙代表隊數據的平均數是75.

(1)求![]() ,
,![]() 的值;
的值;
(2)若分別從甲、乙兩隊隨機各抽取1名成績不低于80分的學生,求抽到的學生中,甲隊學生成績不低于乙隊學生成績的概率;
(3)判斷甲、乙兩隊誰的成績更穩定,并說明理由(方差較小者穩定).
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)甲隊的成績穩定.
;(3)甲隊的成績穩定.
【解析】
(1)因為甲代表隊的中位數為76,其中已知高于76的有77,80,82,88,低于76的有71,71,
65,64,所以![]() ;
;
因為乙代表隊的平均數為75,其中超過75的差值為5,11,13,14,和為43,少于75的差值為3,5,
7,7,19,和為41,所以![]() ;
;
(2)甲隊中成績不低于80的有80,82,88;乙隊中成績不低于80的有80,86,88,89,
乙兩隊各隨機抽取一名,種數為![]() ,
,
其中甲隊學生成績不低于乙隊學生成績的有80,80;82,80;88,80;88,86;88,88.種數為3+1+1=5, 所以甲隊學生成績不低于乙隊學生成績的概率為![]() .
.
(3)因為甲的平均數為
![]() ,
,
所以甲的方差![]()
![]()
![]() ,
,
又乙的方差![]()
![]()
![]() ,
,
因為甲隊的方差小于乙隊的方差,所以甲隊成績較為穩定.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】各項均為非負整數的數列![]() 同時滿足下列條件:
同時滿足下列條件:
①![]()
![]() ;②
;②![]()
![]() ;③
;③![]() 是
是![]() 的因數(
的因數(![]() ).
).
(Ⅰ)當![]() 時,寫出數列
時,寫出數列![]() 的前五項;
的前五項;
(Ⅱ)若數列![]() 的前三項互不相等,且
的前三項互不相等,且![]() 時,
時, ![]() 為常數,求
為常數,求![]() 的值;
的值;
(Ⅲ)求證:對任意正整數![]() ,存在正整數
,存在正整數![]() ,使得
,使得![]() 時,
時, ![]() 為常數.
為常數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“微信運動”已成為當下熱門的運動方式,小王的微信朋友圈內也有大量好友參與了“微信運動”,他隨機選取了其中的40人(男、女各20人),記錄了他們某一天的走路步數,并將數據整理如下:
步數 性別 | 0-2000 | 2001-5000 | 5001-8000 | 8001-10000 | >10000 |
男 | 1 | 2 | 3 | 6 | 8 |
女 | 0 | 2 | 10 | 6 | 2 |
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
附: 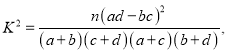
(1)已知某人一天的走路步數超過8000步被系統評定為“積極型”,否則為“懈怠型”,根據題意完成下面的 積極型 懈怠型 總計 男 女 總計 (2)若小王以這40位好友該日走路步數的頻率分布來估計其所有微信好友每日走路步數的概率分布,現從小王的所有微信好友中任選2人,其中每日走路不超過5000步的有![]() 列聯表,并據此判斷能否有95%以上的把握認為“評定類型”與“性別”有關?
列聯表,并據此判斷能否有95%以上的把握認為“評定類型”與“性別”有關?![]() 人,超過10000步的有
人,超過10000步的有![]() 人,設
人,設![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《高中數學課程標準》(2017 版)規定了數學學科的六大核心素養.為了比較甲、乙兩名高二學生的數學核心素養水平,現以六大素養為指標對二人進行了測驗,根據測驗結果繪制了雷達圖(如圖,每項指標值滿分為![]() 分,分值高者為優),則下面敘述正確的是( )
分,分值高者為優),則下面敘述正確的是( )
(注:雷達圖(Radar Chart),又可稱為戴布拉圖、蜘蛛網圖(Spider Chart),可用于對研究對象的多維分析)
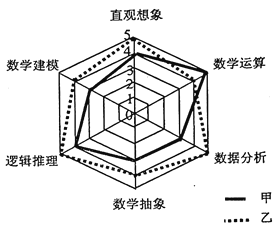
A.甲的數據分析素養高于乙
B.甲的數學建模素養優于數學抽象素養
C.乙的六大素養中邏輯推理最差
D.乙的六大素養整體水平優于甲
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC的內角A,B,C的對邊分別為a,b,c,且asinB=bsin(A+![]() ).
).
(1)求A;
(2)若b,![]() a,c成等差數列,△ABC的面積為2
a,c成等差數列,△ABC的面積為2![]() ,求a.
,求a.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,
中,![]() 點的直角坐標為
點的直角坐標為![]() (
(![]() 為參數).在以原點
為參數).在以原點![]() 為極點,
為極點,![]() 軸正半軸為極軸的極坐標中,直線
軸正半軸為極軸的極坐標中,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.![]() .
.
(1)試求出動點![]() 的軌跡方程(用普通方程表示)
的軌跡方程(用普通方程表示)
(2)設![]() 點對應的軌跡為曲線
點對應的軌跡為曲線![]() ,若曲線
,若曲線![]() 上存在四個點到直線
上存在四個點到直線![]() 的距離為1,求實數
的距離為1,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com