
已知函數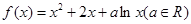 .當
.當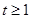 時,不等式
時,不等式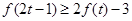 恒成立,則實數
恒成立,則實數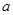 的取值范圍是( )
的取值范圍是( )
A.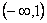 B.
B.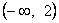 C.
C.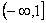 D.
D.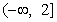
D
【解析】(Ⅱ)∵f(x)=x2+2x+alnx,
∴f(2t-1)≥2f(t)-3⇒2t2-4t+2≥2alnt-aln(2t-1)=aln[t2 /(2t-1 )).
當t≥1時,t2≥2t-1,∴ln[t2 /2t-1 ]≥0.即t>1時,a≤2(t-1)2 /(ln(t2 /2t-1)) 恒成立.又易證ln(1+x)≤x在x>-1上恒成立,
∴(ln(t2 /2t-1)) =ln[1+[(t-1)2/ 2t-1] ]≤(t-1)2 /(2t-1) <(t-1)2在t>1上恒成立.當t=1時取等號,∴當t≥1時,ln(t2 /2t-1) ≤(t-1)2,∴由上知a≤2.故實數a的取值范圍是(-∞,2].


科目:高中數學 來源:2012-2013學年天津市高一(上)期末數學試卷(解析版) 題型:解答題
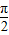 )的圖象如圖所示.
)的圖象如圖所示. 個單位后,再將得到的圖象上各點的橫坐標伸長到原來的4倍,縱坐標不變,得到函數y=g(x)的圖象,求g(x)的對稱軸方程;
個單位后,再將得到的圖象上各點的橫坐標伸長到原來的4倍,縱坐標不變,得到函數y=g(x)的圖象,求g(x)的對稱軸方程;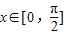 時,方程f(x)=2a-3有兩個不等的實根x1,x2,求實數a的取值范圍,并求此時x1+x2的值.
時,方程f(x)=2a-3有兩個不等的實根x1,x2,求實數a的取值范圍,并求此時x1+x2的值.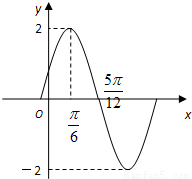
查看答案和解析>>
科目:高中數學 來源:2011-2012學年重慶市高三考前模擬測試理科數學試卷(解析版) 題型:解答題
已知函數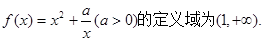
(I)討論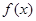 在其定義域上的單調性;
在其定義域上的單調性;
(II)當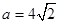 時,若關于x的方程
時,若關于x的方程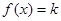 恰有兩個不等實根,求實數k的取值范圍。
恰有兩個不等實根,求實數k的取值范圍。
查看答案和解析>>
科目:高中數學 來源:2011-2012學年福建省高三高考模擬文科數學試卷(解析版) 題型:解答題
(本小題滿分14分)
已知函數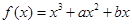
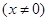 只有一個零點
只有一個零點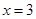 .
.
(Ⅰ)求函數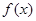 的解析式;
的解析式;
(Ⅱ)若函數 在區間
在區間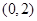 上有極值點,求
上有極值點,求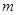 取值范圍;
取值范圍;
(Ⅲ)是否存在兩個不等正數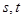
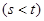 ,當
,當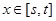 時,函數
時,函數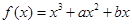 的值域也是
的值域也是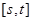 ,若存在,求出所有這樣的正數
,若存在,求出所有這樣的正數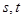 ;若不存在,請說明理由;
;若不存在,請說明理由;
查看答案和解析>>
科目:高中數學 來源: 題型:閱讀理解
(本小題滿分14分)
閱讀下面一段文字:已知數列![]() 的首項
的首項![]() ,如果當
,如果當![]() 時,
時,![]() ,則易知通項
,則易知通項![]() ,前
,前![]() 項的和
項的和![]() . 將此命題中的“等號”改為“大于號”,我們得到:數列
. 將此命題中的“等號”改為“大于號”,我們得到:數列![]() 的首項
的首項![]() ,如果當
,如果當![]() 時,
時,![]() ,那么
,那么![]() ,且
,且![]() . 這種從“等”到“不等”的類比很有趣。由此還可以思考:要證
. 這種從“等”到“不等”的類比很有趣。由此還可以思考:要證![]() ,可以先證
,可以先證![]() ,而要證
,而要證![]() ,只需證
,只需證![]() (
(![]() ). 結合以上思想方法,完成下題:
). 結合以上思想方法,完成下題:
已知函數![]() ,數列
,數列![]() 滿足
滿足![]() ,
,![]() ,若數列
,若數列![]() 的前
的前![]() 項的和為
項的和為![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
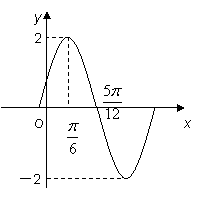
已知函數![]() (其中
(其中![]() )的圖象如圖所示.
)的圖象如圖所示.
(1)求![]() 的解析式;
的解析式;
(2)將函數![]() 的圖象向右平移
的圖象向右平移![]() 個單位后,再將得到的圖象上各點的橫坐標伸長到
個單位后,再將得到的圖象上各點的橫坐標伸長到
原來的![]() 倍,縱坐標不變,得到函數
倍,縱坐標不變,得到函數![]() 的圖象,求
的圖象,求![]() 的對稱軸方程;
的對稱軸方程;
 (3)當
(3)當![]() 時,方程
時,方程![]() 有兩個不等的實根
有兩個不等的實根![]() ,
,![]() ,求實數
,求實數![]() 的取值范圍,
的取值范圍,
并求此時![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com