
分析 (Ⅰ)先解方程得到x=k+$\frac{1}{6}$,或x=k+$\frac{1}{3}$,k∈Z,再分別令n=1,2,即可得到數列{an}的通項公式,
(Ⅱ)bn+1≥a${\;}_{{b}_{n}}$=2bn-$\frac{3}{2}$,利用放縮法得到bn+1-$\frac{3}{2}$≥2n-1,即可得到$\frac{1}{{b}_{n+1}-\frac{3}{2}}$≤$\frac{1}{{2}^{n}}$,求和后再放縮即可證明.
解答 解:(I)由方程$\sqrt{3}$tan2πx-4tanπx+$\sqrt{3}$=0,解得tanπx=$\frac{\sqrt{3}}{3}$,或tanπx=$\sqrt{3}$.
∴πx=kπ+$\frac{π}{6}$,πx=kπ+$\frac{π}{3}$,k∈Z,
即x=k+$\frac{1}{6}$,或x=k+$\frac{1}{3}$,k∈Z.
當n=1時,區間為[0,1),a1=$\frac{1}{6}$+$\frac{1}{3}$=$\frac{1}{2}$,
當n=2時,區間為[1,2),a2=1+$\frac{1}{6}$+1+$\frac{1}{3}$=2+$\frac{1}{2}$=$\frac{5}{2}$,
當x∈[n-1,n),
∴x=$\frac{1}{6}$+(n-1),或x=$\frac{1}{3}$+(n-1),
∴an=$\frac{1}{6}$+(n-1)+$\frac{1}{3}$(n-1)=2n-$\frac{3}{2}$;
(II)證明:由(1)得,bn+1≥a${\;}_{{b}_{n}}$=2bn-$\frac{3}{2}$,
∴bn+1-$\frac{3}{2}$≥a${\;}_{{b}_{n}}$=2bn-$\frac{3}{2}$≥22(bn-1-$\frac{3}{2}$)≥…≥2n(b1-$\frac{3}{2}$)=2n-1>0
∴$\frac{1}{{b}_{n+1}-\frac{3}{2}}$≤$\frac{2}{{2}^{n-1}}$,即$\frac{1}{2{b}_{n+1}-3}$≤$\frac{1}{{2}^{n}}$,
∴$\frac{1}{2{b}_{1}-3}$+$\frac{1}{2{b}_{2}-3}$+…+$\frac{1}{2{b}_{n}-3}$≤1+$\frac{1}{2}$+…+$\frac{1}{{2}^{n-1}}$=$\frac{1×(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$=2-$\frac{1}{{2}^{n-1}}$<2.
點評 本題考查了等比數列的定義通項公式、求和公式、放縮法,考查了推理能力與計算能力,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 3 | B. | 2 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
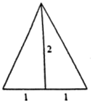
| A. | $\frac{{\sqrt{3}}}{6}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com