
【題目】已知拋物線![]() 的焦點在拋物線
的焦點在拋物線![]() 上,點
上,點![]() 是拋物線
是拋物線![]() 上的動點.
上的動點.
(1)求拋物線![]() 的方程及其準線方程;
的方程及其準線方程;
(2)過點![]() 作拋物線
作拋物線![]() 的兩條切線,
的兩條切線,![]() 、
、![]() 分別為兩個切點,求
分別為兩個切點,求![]() 面積的最小值.
面積的最小值.
【答案】(1)![]() 的方程為
的方程為![]() 其準線方程為
其準線方程為![]() ;(2)2
;(2)2
【解析】試題分析:(1)求得拋物線C1的焦點,由題意可得p=2,即可得到所求拋物線的方程和準線方程;(2)設P(2t,t2),A(x1,y1),B(x2,y2),求出y=x2+1的導數,可得切線PA,PB的斜率和方程,又PA和PB都過P點,可得直線AB的方程,代入拋物線y=x2+1,運用韋達定理和弦長公式,由點到直線的距離公式,可得P到直線AB的距離,再由三角形的面積公式,化簡整理計算可得所求面積的最小值.
試題解析:
(1)![]() 的方程為
的方程為![]() 其準線方程為
其準線方程為![]() .
.
(2)設![]() ,
,![]() ,
,![]() ,
,
則切線![]() 的方程:
的方程:![]() ,即
,即![]() ,又
,又![]() ,
,
所以![]() ,同理切線
,同理切線![]() 的方程為
的方程為![]() ,
,
又![]() 和
和![]() 都過
都過![]() 點,所以
點,所以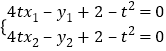 ,
,
所以直線![]() 的方程為
的方程為![]() .
.
聯立![]() 得
得![]() ,所以
,所以![]() 。
。
所以![]() .
.
點![]() 到直線
到直線![]() 的距離
的距離![]() .
.
所以![]() 的面積
的面積![]()
所以當![]() 時,
時, ![]() 取最小值為
取最小值為![]() 。即
。即![]() 面積的最小值為2.
面積的最小值為2.


科目:高中數學 來源: 題型:
【題目】在“新零售”模式的背景下,某大型零售公司為推廣線下分店,計劃在![]() 市
市![]() 區開設分店,為了確定在該區設分店的個數,該公司對該市開設分店的其他區的數據做了初步處理后得到下列表格.記
區開設分店,為了確定在該區設分店的個數,該公司對該市開設分店的其他區的數據做了初步處理后得到下列表格.記![]() 表示在各區開設分店的個數,
表示在各區開設分店的個數,![]() 表示這
表示這![]() 個分店的年收入之和.
個分店的年收入之和.

(1)該公司已經過初步判斷,可用線性回歸模型擬合![]() 與
與![]() 的關系,求
的關系,求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(2)假設該公司在![]() 區獲得的總年利潤
區獲得的總年利潤![]() (單位:百萬元)與
(單位:百萬元)與![]() ,
,![]() 之間的關系為
之間的關系為![]() ,請結合(1)中的線性回歸方程,估算該公司在
,請結合(1)中的線性回歸方程,估算該公司在![]() 區開設多少個分店時,才能使
區開設多少個分店時,才能使![]() 區平均每個分店的年利潤最大?
區平均每個分店的年利潤最大?
參考公式:回歸直線方程為![]() ,其中
,其中 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]()
![]() 上的任一點到焦點的距離最大值為3,離心率為
上的任一點到焦點的距離最大值為3,離心率為![]() ,
,
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若![]() 為曲線
為曲線![]() 上兩點,
上兩點, ![]() 為坐標原點,直線
為坐標原點,直線![]() 的斜率分別為
的斜率分別為![]() ,且
,且![]() ,求直線
,求直線![]() 被圓
被圓![]() 截得弦長的最大值及此時直線
截得弦長的最大值及此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,拋物線
中,拋物線![]() 的頂點是原點,以
的頂點是原點,以![]() 軸為對稱軸,且經過點
軸為對稱軸,且經過點![]() .
.
(Ⅰ)求拋物線![]() 的方程;
的方程;
(Ⅱ)設點![]() ,
, ![]() 在拋物線
在拋物線![]() 上,直線
上,直線![]() ,
, ![]() 分別與
分別與![]() 軸交于點
軸交于點![]() ,
, ![]() ,
, ![]() .求直線
.求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2018四川南充高三第二次(3月)高考適應性考試】某校開展“翻轉合作學習法”教學試驗,經過一年的實踐后,對“翻轉班”和“對照班”的全部220名學生的數學學習情況進行測試,按照大于或等于120分為“成績優秀”,120分以下為“成績一般”統計,得到如下的![]() 列聯表:
列聯表:
成績優秀 | 成績一般 | 合計 | |
對照班 | 20 | 90 | 110 |
翻轉班 | 40 | 70 | 110 |
合計 | 60 | 160 | 220 |
(I)根據上面的列聯表判斷,能否在犯錯誤的概率不超過0.001的前提下認為“成績優秀與翻轉合作學習法”有關;
(II)為了交流學習方法,從這次測試數學成績優秀的學生中,用分層抽樣方法抽出6名學生,再從這6名學生中抽3名出來交流學習方法,求至少抽到1名“對照班”學生交流的概率.
附表:![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校倡導為特困學生募捐,要求在自動購水機處每購買一瓶礦泉水,便自覺向捐款箱中至少投入一元錢.現統計了連續5天的售出礦泉水箱數和收入情況,列表如下:
售出水量 | 7 | 6 | 6 | 5 | 6 |
收入 | 165 | 142 | 148 | 125 | 150 |
學校計劃將捐款以獎學金的形式獎勵給品學兼優的特困生,規定:特困生綜合考核前20名,獲一等獎學金500元;綜合考核21-50名,獲二等獎學金300元;綜合考核50名以后的不獲得獎學金.
(1)若![]() 與
與![]() 成線性相關,則某天售出9箱水時,預計收入為多少元?
成線性相關,則某天售出9箱水時,預計收入為多少元?
(2)甲乙兩名學生獲一等獎學金的概率均為![]() ,獲二等獎學金的概率均為
,獲二等獎學金的概率均為![]() ,不獲得獎學金的概率均為
,不獲得獎學金的概率均為![]() ,已知甲乙兩名學生獲得哪個等級的獎學金相互獨立,求甲乙兩名學生所獲得獎學金之和
,已知甲乙兩名學生獲得哪個等級的獎學金相互獨立,求甲乙兩名學生所獲得獎學金之和![]() 的分布列及數學期望;
的分布列及數學期望;
附:回歸方程![]() ,其中
,其中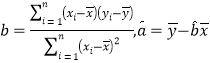 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
, ![]() 滿足約束條件
滿足約束條件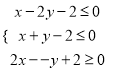 ,若
,若![]() 取得最大值的最優解不唯一,則實數
取得最大值的最優解不唯一,則實數![]() 的值為__________.
的值為__________.
【答案】![]() 或
或![]()
【解析】由題可知若![]() 取得最大值的最優解不唯一則
取得最大值的最優解不唯一則![]() 必平行于可行域的某一邊界,如圖:
必平行于可行域的某一邊界,如圖: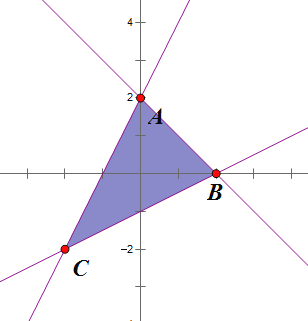 要Z最大則直線與y軸的截距最大即可,當a<0時,則平行AC直線即可故a=-2,當a>0時,則直線平行AB即可,故a=1
要Z最大則直線與y軸的截距最大即可,當a<0時,則平行AC直線即可故a=-2,當a>0時,則直線平行AB即可,故a=1
點睛:線性規劃為常考題型,解決此題務必要理解最優解個數為無數個時的條件是什么,然后根據幾何關系求解即可
【題型】填空題
【結束】
16
【題目】《數書九章》三斜求積術:“以小斜冪,并大斜冪,減中斜冪,余半之,自乘于上;以小斜冪乘大斜冪,減上,余四約一,為實,一為從隅,開平方得積”.秦九韶把三角形的三條邊分別稱為小斜、中斜和大斜,“術”即方法.以![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別表示三角形的面積,大斜,中斜,小斜;
分別表示三角形的面積,大斜,中斜,小斜; ![]() ,
, ![]() ,
, ![]() 分別為對應的大斜,中斜,小斜上的高;則
分別為對應的大斜,中斜,小斜上的高;則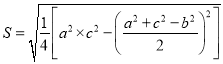
![]()
![]() .若在
.若在![]() 中
中![]() ,
, ![]() ,
, ![]() ,根據上述公式,可以推出該三角形外接圓的半徑為__________.
,根據上述公式,可以推出該三角形外接圓的半徑為__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com