
【題目】如圖,四棱錐P﹣ABCD中,底面ABCD為矩形,PA⊥平面ABCD,AP=1,AD=2,E為線段PD上一點,記 ![]() =λ. 當λ=
=λ. 當λ= ![]() 時,二面角D﹣AE﹣C的平面角的余弦值為
時,二面角D﹣AE﹣C的平面角的余弦值為 ![]() .
. 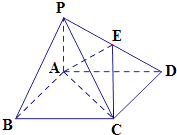
(1)求AB的長;
(2)當 ![]() 時,求異面直線BP與直線CE所成角的余弦值.
時,求異面直線BP與直線CE所成角的余弦值.
【答案】
(1)解:∵PA⊥平面ABCD,ABCD為矩形,∴AB,AD,AP兩兩垂直.
如圖,以A為坐標原點,AB,AD,AP的方向為x軸、y軸、z軸的正方向,
建立空間直角坐標系Axyz,
則D(0,2,0),E(0,1, ![]() ),
), ![]() =(0,1,
=(0,1, ![]() ).
).
設B(m,0,0)(m>0),則C(m,2,0), ![]() =(m,2,0).
=(m,2,0).
設 ![]() =(x,y,z)為平面ACE的法向量,
=(x,y,z)為平面ACE的法向量,
則 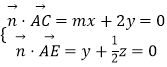 ,取z=2,得
,取z=2,得 ![]() =(
=( ![]() ,﹣1,2).
,﹣1,2).
又 ![]() =(1,0,0)為平面DAE的法向量,
=(1,0,0)為平面DAE的法向量,
∵二面角D﹣AE﹣C的平面角的余弦值為 ![]() ,
,
∴由題設知|cos< ![]() >|=
>|= ![]() ,即
,即 ![]() ,
,
解得m=1,即AB=1
(2)解: ![]() ,
,
∴ ![]() ,
,
![]() ,
, ![]()
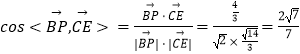 ,
,
∴異面直線BP與直線CE所成角的余弦值為 ![]() .
.
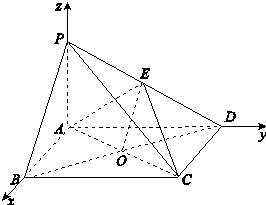
【解析】(1)以A為坐標原點,AB,AD,AP的方向為x軸、y軸、z軸的正方向,建立空間直角坐標系Axyz,利用向量法能求出AB.(2)分別求出 ![]() ,
, ![]() ,利用向量法能求出異面直線BP與直線CE所成角的余弦值.
,利用向量法能求出異面直線BP與直線CE所成角的余弦值.
【考點精析】根據題目的已知條件,利用異面直線及其所成的角的相關知識可以得到問題的答案,需要掌握異面直線所成角的求法:1、平移法:在異面直線中的一條直線中選擇一特殊點,作另一條的平行線;2、補形法:把空間圖形補成熟悉的或完整的幾何體,如正方體、平行六面體、長方體等,其目的在于容易發現兩條異面直線間的關系.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
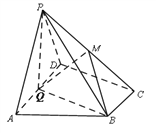
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為直角梯形,
為直角梯形, ![]() ,
, ![]() ,平面
,平面![]() 底面ABCD,Q為AD的中點,M是棱
底面ABCD,Q為AD的中點,M是棱![]() 上的點,
上的點, ![]()
(Ⅰ)若![]() 是棱
是棱![]() 的中點,求證:
的中點,求證: ![]() ;
;
(Ⅱ)若二面角![]() 的大小為
的大小為![]() ,試求
,試求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱ABC﹣A1B1C1中,底面△ABC為等腰直角三角形,∠B=90°,D為棱BB1上一點,且平面DA1C⊥平面AA1C1C. 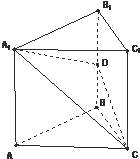
(1)求證:D點為棱BB1的中點;
(2)判斷四棱錐A1﹣B1C1CD和C﹣A1ABD的體積是否相等,并證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,直線
,直線![]() 與橢圓
與橢圓![]() 在第一象限內的交點是
在第一象限內的交點是![]() ,點
,點![]() 在
在![]() 軸上的射影恰好是橢圓
軸上的射影恰好是橢圓![]() 的右焦點
的右焦點![]() ,橢圓
,橢圓![]() 的另一個焦點是
的另一個焦點是![]() ,且
,且![]() .
.
(1) 求橢圓![]() 的方程;
的方程;
(2) 直線![]() 過點
過點![]() ,且與橢圓
,且與橢圓![]() 交于
交于![]() 兩點,求
兩點,求![]() 的內切圓面積的最大值.
的內切圓面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列{an}滿足a1+3a2+32a3+…+3n﹣1an= ![]() (n∈N*).
(n∈N*).
(1)求數列{an}的通項公式;
(2)設bn= ![]() ,求數列{bn}的前n項和Sn .
,求數列{bn}的前n項和Sn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高三(1)班的一次數學測試成績的莖葉圖和頻舉分布直方圖都受到不同程度的破壞,可見部分
如下.


(1)求全班人數及分數在![]() 內的頻數;
內的頻數;
(2)估計該班的平均分數,并計算頻率分布直方圖中![]() 的矩形的高;
的矩形的高;
(3)若要從分數在![]() 內的試卷中任取兩份分析學生的失分情況,在抽取的試卷中,求至少有一份分數在
內的試卷中任取兩份分析學生的失分情況,在抽取的試卷中,求至少有一份分數在![]() 內的概率.
內的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com