
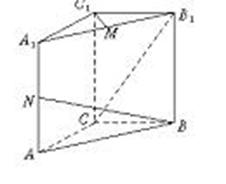
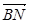 的長; (2)求cos<
的長; (2)求cos<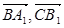 >的值; (3)求證:A1B⊥C1M.
>的值; (3)求證:A1B⊥C1M. 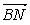 |=
|=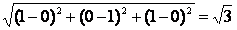 .
.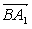 ,
,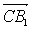 >=
>=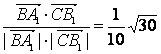 .
. 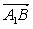 ·
·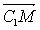 =0,推出A1B⊥C1M。
=0,推出A1B⊥C1M。
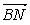 |=
|=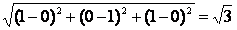 .。。4分
.。。4分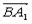 =(1,-1,2),
=(1,-1,2),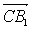 =(0,1,2,),
=(0,1,2,),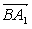 ·
·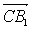 =3,|
=3,|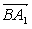 |=
|=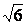 |
|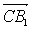 |=
|=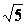
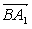 ,
,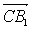 >=
>=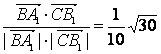 .。。。。。。。8分
.。。。。。。。8分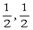 ,2),
,2),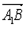 =(-1,1,-2),
=(-1,1,-2),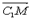 ={
={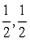 ,0}.∴
,0}.∴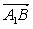 ·
·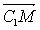 =-
=-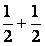 +0=0,∴
+0=0,∴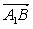 ⊥
⊥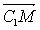 ,∴A1B⊥C1M..。。。。。12分
,∴A1B⊥C1M..。。。。。12分

 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源:不詳 題型:解答題
 中,底面
中,底面 是正方形,側棱
是正方形,側棱 ⊥底面
⊥底面 ,
, ,
, 是
是 的中點,作
的中點,作 交
交 于點
于點
 //平面
//平面 ;
; ⊥平面
⊥平面 ;
; —
— —
— 的大小。
的大小。
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
 是四邊形
是四邊形 所在平面外一點,四邊形
所在平面外一點,四邊形 是
是 的菱形,側面
的菱形,側面
 平面
平面 .
. 為
為 邊的中點,求證:
邊的中點,求證: 平面
平面 .
. .
.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
 、β是兩個不同的平面,則下列命題中正確的是
、β是兩個不同的平面,則下列命題中正確的是A.若m∥n,m∥ ,則n∥ ,則n∥ |
B.若 ⊥β,m∥ ⊥β,m∥ ,則m⊥β ,則m⊥β |
C.若 ⊥β,m⊥β,則m∥ ⊥β,m⊥β,則m∥ |
D.若m⊥n,m⊥ ,n⊥β,則 ,n⊥β,則 ⊥β ⊥β |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:填空題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com