
如圖1,矩形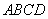 中,
中,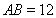 ,
,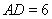 ,
, 、
、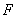 分別為
分別為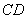 、
、 邊上的點,且
邊上的點,且 ,
,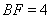 ,將
,將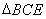 沿
沿 折起至
折起至 位置(如圖2所示),連結
位置(如圖2所示),連結 、
、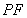 ,其中
,其中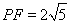 .
.
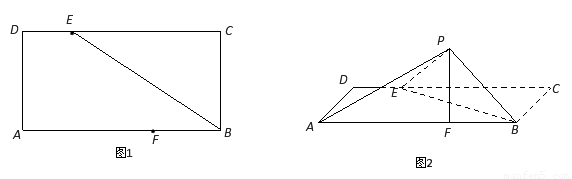
(Ⅰ)求證: 平面
平面 ;
;
(Ⅱ)在線段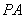 上是否存在點
上是否存在點 使得
使得 平面
平面 ?若存在,求出點
?若存在,求出點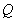 的位置;若不存在,請說明理由.
的位置;若不存在,請說明理由.
(Ⅲ)求點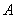 到平面
到平面 的距離.
的距離.
(Ⅰ)答案詳見解析;(Ⅱ)存在, ;(Ⅲ)
;(Ⅲ)  .
.
【解析】
試題分析:(Ⅰ)三角形 和三角形
和三角形 中,各邊長度確定,故可利用勾股定理證明垂直關系
中,各邊長度確定,故可利用勾股定理證明垂直關系
 ,進而由線面垂直的判定定理可證明
,進而由線面垂直的判定定理可證明 平面
平面 ;(Ⅱ)要使得
;(Ⅱ)要使得 平面
平面 ,只需
,只需 ,因為
,因為 ,故
,故 ;(Ⅲ)點到平面的距離,就是點到平面垂線段的長度,如果垂足位置不易確定,可考慮等體積轉化,該題中點
;(Ⅲ)點到平面的距離,就是點到平面垂線段的長度,如果垂足位置不易確定,可考慮等體積轉化,該題中點 到面
到面 的距離確定,故可利用
的距離確定,故可利用 求點
求點 到平面
到平面 的距離.
的距離.
試題解析:(Ⅰ)連結 ,由翻折不變性可知,
,由翻折不變性可知, ,
, ,在
,在 中,
中, ,所以
,所以 , 在圖
, 在圖 中,易得
中,易得 ,
,
在 中,
中, ,所以
,所以 ,又
,又 ,
, 平面
平面 ,
, 平面
平面 ,所以
,所以 平面
平面 .
.

(Ⅱ)當 為
為 的三等分點(靠近
的三等分點(靠近 )時,
)時, 平面
平面 .證明如下:
.證明如下:
因為 ,
, ,所以
,所以 , 又
, 又 平面
平面 ,
, 平面
平面 ,所以
,所以 平面
平面 .
.
(Ⅲ) 由(Ⅰ)知 平面
平面 ,所以
,所以 為三棱錐
為三棱錐 的高.
的高.
設點 到平面
到平面 的距離為
的距離為 ,由等體積法得
,由等體積法得 , 即
, 即 ,又
,又 ,
, , 所以
, 所以 , 即點
, 即點 到平面
到平面 的距離為
的距離為 .
.
考點:1、直線和平面垂直的判定定理;2、直線和平面平行的判定定理;3、點到平面的距離.


 暑假作業海燕出版社系列答案
暑假作業海燕出版社系列答案 本土教輔贏在暑假高效假期總復習云南科技出版社系列答案
本土教輔贏在暑假高效假期總復習云南科技出版社系列答案 暑假作業北京藝術與科學電子出版社系列答案
暑假作業北京藝術與科學電子出版社系列答案科目:高中數學 來源: 題型:
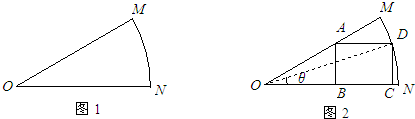 某車間為了制作某個零件,需從一塊扇形的鋼板余料(如圖1)中按照圖2的方式裁剪一塊矩形鋼板ABCD,其中頂點B、C在半徑ON上,頂點A在半徑OM上,頂點D在
某車間為了制作某個零件,需從一塊扇形的鋼板余料(如圖1)中按照圖2的方式裁剪一塊矩形鋼板ABCD,其中頂點B、C在半徑ON上,頂點A在半徑OM上,頂點D在 |
| NM |
| π |
| 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 3 |

查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分14分)如圖, 在矩形![]() 中,
中,![]() ,
,
![]() 分別為線段
分別為線段![]() 的中點,
的中點, ![]() ⊥平面
⊥平面![]() .
.
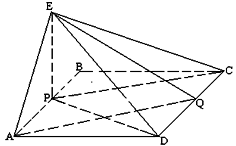 (1) 求證:
(1) 求證: ![]() ∥平面
∥平面![]() ;
;
(2) 求證:平面![]() ⊥平面
⊥平面![]() ;
;
(3) 若![]() , 求三棱錐
, 求三棱錐![]() 的
的
體積.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年江蘇省高三第一學期第二次階段考試數學 題型:解答題
(本小題滿分14分)
1.(本題滿分14分)如圖,矩形 中,
中, ,
, ,
,
 為
為 上的點,且
上的點,且 ,
,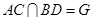 .(Ⅰ)求證:
.(Ⅰ)求證: 平面
平面 ;(Ⅱ)求證:
;(Ⅱ)求證: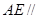 平面
平面 ;(Ⅲ)求三棱錐
;(Ⅲ)求三棱錐 的體積.
的體積.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com