
【題目】某校高三男生體育課上做投籃球游戲,兩人一組,每輪游戲中,每小組兩人每人投籃兩次,投籃投進的次數之和不少于![]() 次稱為“優秀小組”.小明與小亮同一小組,小明、小亮投籃投進的概率分別為
次稱為“優秀小組”.小明與小亮同一小組,小明、小亮投籃投進的概率分別為![]() .
.
(1)若![]() ,
,![]() ,則在第一輪游戲他們獲“優秀小組”的概率;
,則在第一輪游戲他們獲“優秀小組”的概率;
(2)若![]() 則游戲中小明小亮小組要想獲得“優秀小組”次數為
則游戲中小明小亮小組要想獲得“優秀小組”次數為![]() 次,則理論上至少要進行多少輪游戲才行?并求此時
次,則理論上至少要進行多少輪游戲才行?并求此時![]() 的值.
的值.
【答案】(1)![]() (2)理論上至少要進行
(2)理論上至少要進行![]() 輪游戲.
輪游戲.![]()
【解析】
(1)分①小明投中1次,小亮投中2次;②小明投中2次,小亮投中1次;③小明投中2次,小亮投中2次三種情況進行求和即可.
(2)同(1),分別計算三種情況的概率化簡求和,再代入![]() 可知
可知![]() ,再設
,再設![]() ,根據二次函數在區間上的最值方法求解可得當
,根據二次函數在區間上的最值方法求解可得當![]() 時,
時,![]() .再根據他們小組在
.再根據他們小組在![]() 輪游戲中獲“優秀小組”次數
輪游戲中獲“優秀小組”次數![]() 滿足
滿足![]() ,利用二項分布的方法求解即可.
,利用二項分布的方法求解即可.
解:(1)由題可知,所以可能的情況有①小明投中1次,小亮投中2次;②小明投中2次,小亮投中1次;③小明投中2次,小亮投中2次.
故所求概率![]()
(2)他們在一輪游戲中獲“優秀小組”的概率為
![]() 因為
因為![]() ,所以
,所以![]()
因為![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,又
,又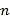
所以![]() ,令
,令![]() ,以
,以![]() ,則
,則![]()
當![]() 時,
時,![]() ,他們小組在
,他們小組在![]() 輪游戲中獲“優秀小組”次數
輪游戲中獲“優秀小組”次數![]() 滿足
滿足![]()
由![]() ,則
,則![]() ,所以理論上至少要進行
,所以理論上至少要進行![]() 輪游戲.此時
輪游戲.此時![]() ,
,![]() ,
,![]()


 特高級教師點撥系列答案
特高級教師點撥系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,點
,點![]() ,
,![]() ,
,![]() 分別是橢圓
分別是橢圓![]() 的左、右焦點,
的左、右焦點,![]() 為等腰三角形.
為等腰三角形.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)過左焦點![]() 作直線
作直線![]() 交橢圓于
交橢圓于![]() 兩點,其中
兩點,其中![]()
![]() ,另一條過
,另一條過![]() 的直線
的直線![]() 交橢圓于
交橢圓于![]() 兩點(不與
兩點(不與![]() 重合),且
重合),且![]() 點不與點
點不與點![]() 重合. 過
重合. 過![]() 作
作![]() 軸的垂線分別交直線
軸的垂線分別交直線![]() ,
,![]() 于
于![]() ,
,![]() .
.
①求![]() 點坐標; ②求證:
點坐標; ②求證:.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).以原點
為參數).以原點![]() 為極點,以
為極點,以![]() 軸為非負半軸為極軸建立極坐標系,兩坐標系相同的長度單位.圓
軸為非負半軸為極軸建立極坐標系,兩坐標系相同的長度單位.圓![]() 的方程為
的方程為![]() 被圓
被圓![]() 截得的弦長為
截得的弦長為![]() .
.
(Ⅰ)求實數![]() 的值;
的值;
(Ⅱ)設圓![]() 與直線
與直線![]() 交于點
交于點![]() ,若點
,若點![]() 的坐標為
的坐標為![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高三男生體育課上做投籃球游戲,兩人一組,每輪游戲中,每小組兩人每人投籃兩次,投籃投進的次數之和不少于![]() 次稱為“優秀小組”.小明與小亮同一小組,小明、小亮投籃投進的概率分別為
次稱為“優秀小組”.小明與小亮同一小組,小明、小亮投籃投進的概率分別為![]() .
.
(1)若![]() ,
,![]() ,則在第一輪游戲他們獲“優秀小組”的概率;
,則在第一輪游戲他們獲“優秀小組”的概率;
(2)若![]() 則游戲中小明小亮小組要想獲得“優秀小組”次數為
則游戲中小明小亮小組要想獲得“優秀小組”次數為![]() 次,則理論上至少要進行多少輪游戲才行?并求此時
次,則理論上至少要進行多少輪游戲才行?并求此時![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,其焦距為
,其焦距為![]() ,點E為橢圓的上頂點,且
,點E為橢圓的上頂點,且![]() .
.
(1)求橢圓C的方程;
(2)設圓![]() 的切線l交橢圓C于A,B兩點(O為坐標原點),求證
的切線l交橢圓C于A,B兩點(O為坐標原點),求證![]() ;
;
(3)在(2)的條件下,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有一片產量很大的水果種植園,在臨近成熟時隨機摘下某品種水果100個,其質量(均在l至11kg)頻數分布表如下(單位: kg):
分組 | | | | | |
頻數 | 10 | 15 | 45 | 20 | 10 |
以各組數據的中間值代表這組數據的平均值,將頻率視為概率.
(1)由種植經驗認為,種植園內的水果質量![]() 近似服從正態分布
近似服從正態分布![]() ,其中
,其中![]() 近似為樣本平均數
近似為樣本平均數![]() 近似為樣本方差
近似為樣本方差![]() .請估算該種植園內水果質量在
.請估算該種植園內水果質量在![]() 內的百分比;
內的百分比;
(2)現在從質量為![]() 的三組水果中用分層抽樣方法抽取14個水果,再從這14個水果中隨機抽取3個.若水果質量
的三組水果中用分層抽樣方法抽取14個水果,再從這14個水果中隨機抽取3個.若水果質量![]() 的水果每銷售一個所獲得的的利潤分別為2元,4元,6元,記隨機抽取的3個水果總利潤為
的水果每銷售一個所獲得的的利潤分別為2元,4元,6元,記隨機抽取的3個水果總利潤為![]() 元,求
元,求![]() 的分布列及數學期望.
的分布列及數學期望.
附:![]()
![]() ,則
,則![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了迎接2019年全國文明城市評比,某市文明辦對市民進行了一次文明創建知識的網絡問卷調查.每一位市民有且僅有一次參加機會,通過隨機抽樣,得到參加問卷調查的1000人的得分(滿分:100分)數據,統計結果如下表所示:
組別 |
|
|
|
|
|
|
|
頻數 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
(1)由頻數分布表可以認為,此次問卷調查的得分![]() 服從正態分布
服從正態分布![]() ,
,![]() 近似為這1000人得分的平均值(同一組數據用該組區間的中點值作為代表),請利用正態分布的知識求
近似為這1000人得分的平均值(同一組數據用該組區間的中點值作為代表),請利用正態分布的知識求![]() ;
;
(2)在(1)的條件下,文明辦為此次參加問卷調查的市民制定如下獎勵方案:
(i)得分不低于![]() 的可以獲贈2次隨機話費,得分低于
的可以獲贈2次隨機話費,得分低于![]() 的可以獲贈1次隨機話費;
的可以獲贈1次隨機話費;
(ii)每次獲贈的隨機話費和對應的概率為:
獲贈的隨機話費(單位:元) | 20 | 40 |
概率 |
|
|
現市民小王要參加此次問卷調查,記![]() (單位:元)為該市民參加問卷調查獲贈的話費,求
(單位:元)為該市民參加問卷調查獲贈的話費,求![]() 的分布列及數學期望.
的分布列及數學期望.
附:①![]() ;
;
②若![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱柱ABC﹣A1B1C1中,M,M1分別為AB,A1B1中點.
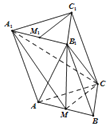
(1)求證:C1M1∥面A1MC;
(2)若面ABC⊥面ABB1A1,△AB1B為正三角形,AB=2,BC=1,![]() ,求四棱錐B1﹣AA1C1C的體積.
,求四棱錐B1﹣AA1C1C的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com