
 ,P是橢圓C在第一象限內的一點,且|PF1|-|PF2|=1.
,P是橢圓C在第一象限內的一點,且|PF1|-|PF2|=1. 解:(1)依題可設橢圓方程為
解:(1)依題可設橢圓方程為
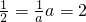 ,b2=a2-12=3-------------(2分)
,b2=a2-12=3-------------(2分) .-------------------(3分)
.-------------------(3分) -------(2分)
-------(2分) 得
得 或
或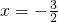 (舍去)
(舍去) -------------------(4分)
-------------------(4分)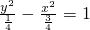 -------------------(2分)
-------------------(2分) 得
得 ------------------(3分)
------------------(3分)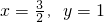 ∴
∴ -------------------(4分)
-------------------(4分) -------------------(1分)
-------------------(1分) ,得s=0-------------------(2分)
,得s=0-------------------(2分) ,∴t=±2-------------------(3分)
,∴t=±2-------------------(3分) ,∴
,∴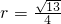 ,
,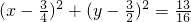 -------------(6分)
-------------(6分)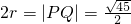 ,∴
,∴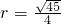 ,∴圓G為:
,∴圓G為: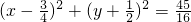 ------------(7分)
------------(7分)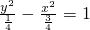 的上支,從而可得P為橢圓與雙曲線的交點,聯立
的上支,從而可得P為橢圓與雙曲線的交點,聯立 ,
,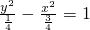 可求
可求 可求Q
可求Q 或
或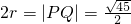 ,,從而可得圓的方程
,,從而可得圓的方程

科目:高中數學 來源: 題型:
| 1 |
| 2 |
| AF2 |
| F2B |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源:2011年廣東省汕頭市高三質量測評數學試卷2(理科)(解析版) 題型:解答題
 ,P是橢圓C在第一象限內的一點,且|PF1|-|PF2|=1.
,P是橢圓C在第一象限內的一點,且|PF1|-|PF2|=1.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com