
【題目】選做題:幾何證明選講 如圖,ABCD是邊長為a的正方形,以D為圓心,DA為半徑的圓弧與以BC為直徑的半圓O交于點F,延長CF交AB于E.
(1)求證:E是AB的中點;
(2)求線段BF的長.
科目:高中數學 來源: 題型:
【題目】函數f(x)=sinωx(>0)的圖象向右平移 ![]() 個單位得到函數y=g(x)的圖象,并且函數g(x)在區間[
個單位得到函數y=g(x)的圖象,并且函數g(x)在區間[ ![]() ,
, ![]() ]上單調遞增,在區間[
]上單調遞增,在區間[ ![]() ]上單調遞減,則實數ω的值為( )
]上單調遞減,則實數ω的值為( )
A.![]()
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正項數列![]() 的前
的前![]() 項和為
項和為![]() ,滿足
,滿足![]() .
.
(Ⅰ)(i)求數列![]() 的通項公式;
的通項公式;
(ii)已知對于![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的最小值;
的最小值;
(Ⅱ) 數列![]() 的前
的前![]() 項和為
項和為![]() ,滿足
,滿足![]() ,是否存在非零實數
,是否存在非零實數![]() ,使得數列
,使得數列![]() 為等比數列? 并說明理由.
為等比數列? 并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)定義域為R,f(﹣x)=f(x),f(x)=f(2﹣x),當x∈[0,1]時,f(x)=x3 , 則函數g(x)=|cos(πx)|﹣f(x)在區間[﹣ ![]() ,
, ![]() ]上的所有零點的和為 .
]上的所有零點的和為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD是菱形,且∠DAB=60°.點E是棱PC的中點,平面ABE與棱PD交于點F. (Ⅰ)求證:AB∥EF;
(Ⅱ)若PA=PD=AD,且平面PAD⊥平面ABCD,求平面PAF與平面AFE所成的銳二面角的余弦值.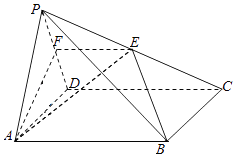
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數f(x)= ![]() x2﹣lnx在其定義域的一個子區間(k﹣1,k+1)上不是單調函數,則實數k的取值范圍是( )
x2﹣lnx在其定義域的一個子區間(k﹣1,k+1)上不是單調函數,則實數k的取值范圍是( )
A.(1,2)
B.[1,2)
C.[0,2)
D.(0,2)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于任意![]() ,若數列
,若數列![]() 滿足
滿足![]() ,則稱這個數列為“
,則稱這個數列為“![]() 數列”.
數列”.
(1)已知數列:![]() ,
,![]() ,
,![]() 是“
是“![]() 數列”,求實數
數列”,求實數![]() 的取值范圍;
的取值范圍;
(2)已知等差數列![]() 的公差
的公差![]() ,前
,前![]() 項和為
項和為![]() ,數列
,數列![]() 是“
是“![]() 數列”,求首項
數列”,求首項![]() 的取值范圍;
的取值范圍;
(3)設數列![]() 的前
的前![]() 項和為
項和為![]() ,
,![]() ,且
,且![]() ,
,![]() . 設
. 設![]() ,是否存在實數
,是否存在實數![]() ,使得數列
,使得數列![]() 為“
為“![]() 數列”. 若存在,求實數
數列”. 若存在,求實數![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com