
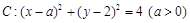 及直線
及直線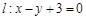 . 當直線
. 當直線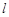 被圓
被圓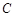 截得的弦長為
截得的弦長為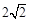 時, 求(1)
時, 求(1)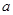 的值; (2)求過點
的值; (2)求過點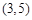 并與圓
并與圓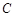 相切的切線方程.
相切的切線方程. ;(2)
;(2) 或
或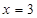
 的距離
的距離 ,可列式為
,可列式為 ,進而求
,進而求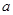 ;(2)先利用點斜式方程設直線為
;(2)先利用點斜式方程設直線為 ,因為直線和圓相切,利用
,因為直線和圓相切,利用 求參數
求參數 ,因為點
,因為點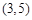 在圓外,所以切線可引兩條,則會想到另一條直線必是斜率不存在 情況,再補
在圓外,所以切線可引兩條,則會想到另一條直線必是斜率不存在 情況,再補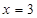 .
.
 ,則圓心到直線
,則圓心到直線 的距離
的距離 ,由勾股定理可知
,由勾股定理可知 ,代入化簡得
,代入化簡得 ,解得
,解得 ,又
,又 ,所以
,所以 ;
;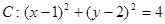 , 又
, 又 在圓外,
在圓外, ①當切線方程的斜率存在時,設方程為
①當切線方程的斜率存在時,設方程為 ,由圓心到切線的距離
,由圓心到切線的距離 可解得
可解得 ,
, 切線方程為
切線方程為 ……9分,②當過
……9分,②當過 斜率不存在,易知直線
斜率不存在,易知直線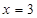 與圓相切,綜合①②可知切線方程為
與圓相切,綜合①②可知切線方程為 或
或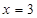 .
.

 學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案
學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案 芒果教輔暑假天地重慶出版社系列答案
芒果教輔暑假天地重慶出版社系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com