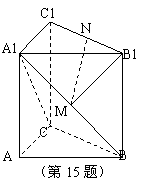
如圖，直三棱柱ABC-A1B1C1中，∠ACB=90°，M，N分別為A1B，B1C1的中點．
（1）求證BC∥平面MNB1；
（2）求證平面A1CB⊥平面ACC1A1．
（本小題滿分12分）
如圖，直三棱柱ABC-A1B1C1中，∠ACB=90°，
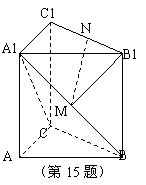M，N分別為A1B，B1C1的中點．
（1）求證BC∥平面MNB1；
（2）求證平面A1CB⊥平面ACC1A1．
答案：（1）因BC∥B1C1， ………………………………………………………………………2分
且B1C1
平面MNB1， …………………………………………………………………………4分
BC
平面MNB1，
故BC∥平面MNB1． …………………………………………………………………………6分
（2）因BC⊥AC，且ABC-A1B1C1為直三棱柱， ……………………………………………8分
故BC⊥平面ACC1A1．
因BC平面A1CB， ……………………………………………………………………………10分
故平面A1CB⊥平面ACC1A1． …………………………………………………………………12分
講評建議：必修2中的立幾初步，必須控制難度，注重答題規范．
桃李文化快樂暑假武漢出版社系列答案科目：高中數學 來源： 題型：
如圖，直三棱柱ABC-A1B1C1中，∠ACB=90°，AC=1，CB=| 2 |
查看答案和解析>>
科目：高中數學 來源： 題型：
如圖，直三棱柱ABC-A1B1C1中，底面是以∠ABC為直角的等腰直角三角形，AC=2a，BB1=3a，D為A1C1的中點，E為B1C的中點．| AF |
查看答案和解析>>
科目：高中數學 來源： 題型：
如圖，直三棱柱ABC-A1B1C1中，AC⊥BC，AC=BC=CC1=2，M，N分別為AC，B1C1的中點．查看答案和解析>>
科目：高中數學 來源： 題型：
如圖，直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=a，AA1=2a，D棱B1B的中點．查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
如圖在直三棱柱ABC-A1B1C1中∠ACB=90°，AA1=2，AC=BC=1，則異面直線A1B與AC所成角的余弦值是