
【題目】已知函數f(x)=ax3﹣bx+2(a>0)
(1)在x=1時有極值0,試求函數f(x)的解析式;
(2)求f(x)在x=2處的切線方程.
【答案】
(1)解:函數f(x)=ax3﹣bx+2的導數為f′(x)=3ax2﹣b,
在x=1時有極值0,可得f(1)=0,且f′(1)=0,
即為a﹣b+2=0,且3a﹣b=0,
解得a=1,b=3,
可得f(x)=x3﹣3x+2
(2)解:f′(x)=3ax2﹣b,
可得f(x)在x=2處的切線斜率為12a﹣b,
切點為(2,8a﹣2b+2),
即有f(x)在x=2處的切線方程為y﹣(8a﹣2b+2)=(12a﹣b)(x﹣2),
化為(12a﹣b)x﹣y﹣16a+2=0
【解析】(1)求出f(x)的導數,可得f(1)=0,且f′(1)=0,得到a,b的方程,解方程可得a,b的值,進而得到f(x)的解析式;(2)求出f(x)的導數,可得切線的斜率和切點,由點斜式方程即可得到所求切線的方程.
【考點精析】本題主要考查了函數的極值與導數的相關知識點,需要掌握求函數![]() 的極值的方法是:(1)如果在
的極值的方法是:(1)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極大值(2)如果在
是極大值(2)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極小值才能正確解答此題.
是極小值才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐 ![]() 中,平面
中,平面 ![]() 平面
平面 ![]() ,
, ![]() 為等邊三角形,
為等邊三角形, ![]() 且
且 ![]() ,
, ![]() 分別為
分別為 ![]() 的中點.
的中點.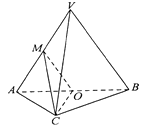
(1)求證: ![]() 平面
平面 ![]() .
.
(2)求證:平面 ![]() 平面
平面 ![]() .
.
(3)求三棱錐 ![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設命題p:x0∈(0,+∞),3 ![]() +x0=2016,命題q:a∈(0,+∞),f(x)=|x|﹣ax,(x∈R)為偶函數,那么,下列命題為真命題的是( )
+x0=2016,命題q:a∈(0,+∞),f(x)=|x|﹣ax,(x∈R)為偶函數,那么,下列命題為真命題的是( )
A.p∧q
B.(¬p)∧q
C.p∧(¬q)
D.(¬p)∧(¬q)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y=f(x)對任意的x∈(﹣ ![]() ,
, ![]() )滿足f′(x)cosx+f(x)sinx>0(其中f′(x)是函數f(x)的導函數),則下列不等式成立的是 . ①
)滿足f′(x)cosx+f(x)sinx>0(其中f′(x)是函數f(x)的導函數),則下列不等式成立的是 . ① ![]() f(﹣
f(﹣ ![]() )<f(﹣
)<f(﹣ ![]() )
)
② ![]() f(
f( ![]() )<f(
)<f( ![]() )
)
③f(0)>2f( ![]() )
)
④f(0)> ![]() f(
f( ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,四棱錐P﹣ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD,PA=AD=AB= ![]() CD=1,M為PB的中點.
CD=1,M為PB的中點. 
(1)試在CD上確定一點N,使得MN∥平面PAD;
(2)點N在滿足(1)的條件下,求直線MN與平面PAB所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知 ![]() 表示兩條不同的直線,
表示兩條不同的直線, ![]() 表示一個平面,給出下列四個命題:
表示一個平面,給出下列四個命題:
① ![]() ;②
;② ![]() ;
;
③ ![]() ;④
;④ ![]() .
.
其中正確命題的序號是( )
A.①②
B.②③
C.②④
D.①④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com