已知正方形ABCD所在平面與正方形ABEF所在平面互相垂直,M為AC上一點,N為BF上一點,且AM=FN=x有,設AB=a
(1)求證:MN∥平面CBE;
(2)求證:MN⊥AB;
(3)當x為何值時,MN取最小值?并求出這個最小值.
分析:(1)先由
==相似性推知
MGNH得出MNHG為平行四邊形,從而求證MN∥GH,由線面平行的判定定理證得MN∥面BEC;(2)由AB⊥BC,AB⊥BE,結合線面垂直的判定定理證出AB⊥面BEC,從而有AB⊥GH,再由垂直于平行線中的一條,則垂直于另一條,得到MN⊥AB;
(3)由面ABCD⊥面ABEF,得到BE⊥面ABCD,從而有BE⊥BC,BG=
,BH=
,建立MN=GH=
二次函數模型從而求得最值.
解答:證明:(1)在平面ABC中,作MG∥AB,在平面BFE中,作NH∥EF,
連接GH∵AM=FN∴MC=NB∵
==∴
MGNH∴MNHG為平行四邊形;∴MN∥GH
又∵GH⊆面BEC,MN
≠?面BEC∴MN∥面BEC
(2)∵AB⊥BC,AB⊥BE∴AB⊥面BEC∵GH⊆面GEC∴AB⊥GH∵MN∥GH∴MN⊥AB
(3)∵面ABCD⊥面ABEF∴BE⊥面ABCD∴BE⊥BC
∵BG=
,BH=
∴MN=GH=
=
=
(
0<a<a)
=
≤a當且僅當
x=a時,等號成立;
∴當
x=a時,MN取最小值
a.
點評:本題主要通過平面圖形中的相似性轉化線線平行,進而轉化為線面平行來考查線面平行的判定定理,以及線面垂直的判定和培養學生平面和空間的轉化及建模能力.



 如圖,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF=
如圖,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF= 已知正方形ABCD邊長為1,圖形如示,點E為邊BC的中點,正方形內部一動點P滿足:P到線段AD的距離等于P到點E的距離,那么P點的軌跡與正方形的上、下底邊及BC邊所圍成平面圖形的面積為
已知正方形ABCD邊長為1,圖形如示,點E為邊BC的中點,正方形內部一動點P滿足:P到線段AD的距離等于P到點E的距離,那么P點的軌跡與正方形的上、下底邊及BC邊所圍成平面圖形的面積為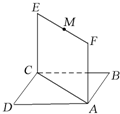 (2010•煙臺一模)如圖,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
(2010•煙臺一模)如圖,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=