
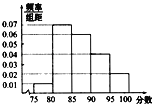
【題目】某校在2013年的自主招生考試成績中隨機抽取40名學生的筆試成績,按成績共分成五組:第1組[75,80),第2組[80,85),第3組[85,90),第4組[90,95),第5組[95,100],得到的頻率分布直方圖如圖所示,同時規定成績在85分以上的學生為“優秀”,成績小于85分的學生為“良好”,且只有成績為“優秀”的學生才能獲得面試資格.

(1)求出第4組的頻率,并補全頻率分布直方圖;
(2)根據樣本頻率分布直方圖估計樣本的中位數與平均數;
(3)如果用分層抽樣的方法從“優秀”和“良好”的學生中共選出5人,再從這5人中選2人,那么至少有一人是“優秀”的概率是多少?
【答案】(1)第4組的頻率為0.2,作圖見解析(2)樣本中位數的估計值為![]() ,平均數為87.25(3)0.9
,平均數為87.25(3)0.9
【解析】
(1)利用頻率和為1,計算可得答案,計算可得第四個矩形的高度為0.2÷5=0.04,由此作圖即可;
(2) 設樣本的中位數為x,由5×0.01+5×0.07+(x﹣85)×0.06=0.5解出![]() 即可得到中位數,根據77.5×0.05+82.5×0.35+87.5×0.30+92.5×0.20+97.5×0.10計算即可得到平均數;
即可得到中位數,根據77.5×0.05+82.5×0.35+87.5×0.30+92.5×0.20+97.5×0.10計算即可得到平均數;
(3)通過列舉法可得所有基本事件的總數以及至少有一人是“優秀”的總數,再利用古典概型概率公式計算可得.
(1)其它組的頻率為(0.01+0.07+0.06+0.02)×5=0.8,所以第4組的頻率為0.2,
頻率分布圖如圖:
(2)設樣本的中位數為x,則5×0.01+5×0.07+(x﹣85)×0.06=0.5,解得x![]() ,
,
∴樣本中位數的估計值為![]() ,
,
平均數為77.5×0.05+82.5×0.35+87.5×0.30+92.5×0.20+97.5×0.10=87.25;
(3)依題意良好的人數為40×0.4=16人,優秀的人數為40×0.6=24人
優秀與良好的人數比為3:2,所以采用分層抽樣的方法抽取的5人中有優秀3人,良好2人,
記“從這5人中選2人至少有1人是優秀”為事件M,
將考試成績優秀的三名學生記為A,B,C,考試成績良好的兩名學生記為a,b,
從這5人中任選2人的所有基本事件包括:
AB,AC,BC,Aa,Ab,Ba,Bb,Ca,Cb,ab共10個基本事件,
事件M含的情況是:AB,AC,BC,Aa,Ab,Ba,Bb,Ca,Cb,共9個,
所以P(M)![]() 0.9.
0.9.


 優加精卷系列答案
優加精卷系列答案科目:高中數學 來源: 題型:
【題目】在![]() 中,有正弦定理:
中,有正弦定理:![]() 定值,這個定值就是
定值,這個定值就是![]() 的外接圓的直徑
的外接圓的直徑![]() 如圖2所示,
如圖2所示,![]() 中,已知
中,已知![]() ,點M在直線EF上從左到右運動
,點M在直線EF上從左到右運動![]() 點M不與E、F重合
點M不與E、F重合![]() ,對于M的每一個位置,記
,對于M的每一個位置,記![]() 的外接圓面積與
的外接圓面積與![]() 的外接圓面積的比值為
的外接圓面積的比值為![]() ,那么
,那么![]()
![]()

A. ![]() 先變小再變大
先變小再變大
B. 僅當M為線段EF的中點時,![]() 取得最大值
取得最大值
C. ![]() 先變大再變小
先變大再變小
D. ![]() 是一個定值
是一個定值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點F為拋物線C:x2=2py (p>0) 的焦點,點A(m,3)在拋物線C上,且|AF|=5,若點P是拋物線C上的一個動點,設點P到直線![]() 的距離為
的距離為![]() ,設點P到直線
,設點P到直線![]() 的距離為
的距離為![]() .
.
(1)求拋物線C的方程;
(2) 求![]() 的最小值;
的最小值;
(3)求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點分別為
的兩個焦點分別為![]() ,
,![]() ,離心率為
,離心率為![]() ,且橢圓四個頂點構成的菱形面積為
,且橢圓四個頂點構成的菱形面積為![]() .
.
(1)求橢圓C的方程;
(2)若直線l :y=x+m與橢圓C交于M,N兩點,以MN為底邊作等腰三角形,頂點為P(3,-2),求m的值及△PMN的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,
,![]() 分別是橢圓
分別是橢圓![]()
![]() 的長軸端點、短軸端點,
的長軸端點、短軸端點,![]() 為坐標原點,若
為坐標原點,若![]() ,
,![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)如果斜率為![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于不同的兩點
于不同的兩點![]() (都不同于點
(都不同于點![]() ),線段
),線段![]() 的中點為
的中點為![]() ,設線段
,設線段![]() 的垂線
的垂線![]() 的斜率為
的斜率為![]() ,試探求
,試探求![]() 與
與![]() 之間的數量關系.
之間的數量關系.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從8名運動員中選4人參加![]() 米接力賽,在下列條件下,各有多少種不同的排法?
米接力賽,在下列條件下,各有多少種不同的排法?
(1)甲、乙兩人必須入選且跑中間兩棒;
(2)若甲、乙兩人只有一人被選且不能跑中間兩棒;
(3)若甲、乙兩人都被選且必須跑相鄰兩棒;
(4)甲不在第一棒.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】△ABC的內角A,B,C所對應的邊分別為a,b,c.
(Ⅰ)若a,b,c成等差數列,證明:sinA+sinC=2sin(A+C);
(Ⅱ)若a,b,c成等比數列,求cosB的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com