
【題目】若函數![]() 滿足下列條件:在定義域內存在
滿足下列條件:在定義域內存在![]() ,使得
,使得![]() 成立,則稱函數
成立,則稱函數![]() 具有性質
具有性質![]() ;反之,若
;反之,若![]() 不存在,則稱函數
不存在,則稱函數![]() 不具有性質
不具有性質![]() .
.
(Ⅰ)證明:函數![]() 具有性質
具有性質![]() ,并求出對應的
,并求出對應的![]() 的值;
的值;
(Ⅱ)試分別探究形如①![]() (
(![]() )、②
)、②![]() (
(![]() 且
且![]() )、③
)、③![]() (
(![]() 且
且![]() )的函數,是否一定具有性質
)的函數,是否一定具有性質![]() ?并加以證明.
?并加以證明.
(Ⅲ)已知函數![]() 具有性質
具有性質![]() ,求
,求![]() 的取值范圍;
的取值范圍;
【答案】(Ⅰ)證明見解析;(Ⅱ)見解析;(Ⅲ) ![]()
【解析】試題分析:(Ⅰ)把函數![]() 代入
代入![]() ,解出
,解出![]() 從而求解;
從而求解;
(Ⅱ)函數![]() 恒具有性質
恒具有性質![]() ,即關于的方程
,即關于的方程![]() 恒有解.
恒有解.
分別探究形如①![]() (
(![]() )、②
)、②![]() (
(![]() 且
且![]() )、③
)、③![]() (
(![]() 且
且![]() )的函數,把其代入進行一一驗證是否具有性質M;
)的函數,把其代入進行一一驗證是否具有性質M;
(Ⅲ)根據![]() 具有性質
具有性質![]() ,即存在x0,使得存在
,即存在x0,使得存在![]() ,使得
,使得![]() ,代入得到一個關于
,代入得到一個關于![]() 的方程,其中含有參數
的方程,其中含有參數![]() ,并對
,并對![]() 進行討論,從而求出
進行討論,從而求出![]() 的取值范圍;
的取值范圍;
試題解析:(Ⅰ)證明: ![]() 代入
代入![]() 得:
得:
![]()
即![]() ,解得
,解得![]() ∴函數
∴函數![]() 具有性質
具有性質![]() .
.
(Ⅱ)函數![]() 恒具有性質
恒具有性質![]() ,即關于的方程
,即關于的方程![]() (*)恒有解.
(*)恒有解.
①若![]() (
(![]() ),則方程(*)可化為
),則方程(*)可化為![]() ,解得
,解得![]() .
.
∴函數![]() (
(![]() )一定具備性質
)一定具備性質![]() .
.
②若![]() ,則方程(*)可化為
,則方程(*)可化為![]() ,化簡得
,化簡得![]() 即
即![]()
當![]() 時,方程(*)無解
時,方程(*)無解
∴函數![]() (
(![]() 且
且![]() )不一定具有性質
)不一定具有性質![]() .
.
③若![]() ,則方程(*)可化為
,則方程(*)可化為![]() ,化簡得
,化簡得![]() 顯然方程無解
顯然方程無解
∴函數![]() (
(![]() 且
且![]() )不一定具有性質
)不一定具有性質![]() .
.
(Ⅲ)解: ![]() 的定義域為
的定義域為![]() ,且可得
,且可得![]() ,∵
,∵![]() 具有性質
具有性質![]() ,
,
∴存在![]() ,使得
,使得![]() ,代入得
,代入得![]() 化為
化為![]()
整理得: ![]() 有實根
有實根
①若![]() ,得
,得![]() ,滿足題意;
,滿足題意;
②若![]() ,則要使
,則要使![]() 有實根,只需滿足
有實根,只需滿足![]() ,即
,即![]() ,解得
,解得![]()
∴![]()
綜合①②,可得![]()


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2-3x+lnx.
(Ⅰ)求函數f(x)的極值;
(Ⅱ)若對于任意的x1,x2∈(1,+∞),x1≠x2,都有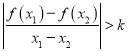 恒成立,求實數k的取值范圍.
恒成立,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三條直線l1:4x+y-4=0,l2:mx+y=0,l3:2x-3my-4=0.
(1)若直線l1,l2,l3交于一點,求實數m的值;
(2)若直線l1,l2,l3不能圍成三角形,求實數m的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來空氣質量逐步惡化,霧霾天氣現象增多,大氣污染危害加重.大氣污染可引起心悸、呼吸困難等心肺疾病.為了解心肺疾病是否與性別有關,在市第一人民醫院隨機對入院50人進行了問卷調查,得到如下的列聯表:
患心肺疾病 | 不患心肺疾病 | 合計 | |
男 | 20 | 5 | 25 |
女 | 10 | 15 | 25 |
合計 | 30 | 20 | 50 |
(1)是否有99.5%的把握認為患心肺疾病與性別有關?說明你的理由;
(2)已知在患心肺疾病的10位女性中,有3位又患有胃病,現在從患心肺疾病的10位女性中,選出3位進行其他方面的排查,其中患胃病的人數為![]() ,求
,求![]() 的分布列、數學期望.
的分布列、數學期望.
參考公式: 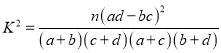 ,其中
,其中![]() .
.
下面的臨界值僅供參考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,直線l過點P (3, ![]() )且傾斜角為
)且傾斜角為![]() .在極坐標系(與直角坐標系xOy取相同的長度單位,且以原點O為極點,以x軸正半軸為極軸)中,圓C的方程為
.在極坐標系(與直角坐標系xOy取相同的長度單位,且以原點O為極點,以x軸正半軸為極軸)中,圓C的方程為![]() .
.
(Ⅰ)求直線l的一個參數方程和圓C的直角坐標方程;
(Ⅱ)設圓C與直線l交于點A,B,求![]() 的值.
的值.
(2)已知函數![]() .
.
(Ⅰ)求函數![]() 的最小值
的最小值![]() ;
;
(Ⅱ)若正實數![]() 滿足
滿足![]() ,且
,且![]() 對任意的正實數
對任意的正實數![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某超市從現有甲、乙兩種酸奶的日銷售量(單位:箱)的1200個數據(數據均在區間![]() 內)中,按照5%的比例進行分層抽樣,統計結果按
內)中,按照5%的比例進行分層抽樣,統計結果按![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分組,整理如下圖:
分組,整理如下圖:
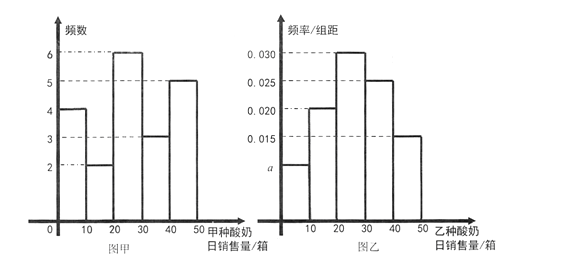
(Ⅰ)寫出頻率分布直方圖(圖乙)中![]() 的值;記所抽取樣本中甲種酸奶與乙種酸奶日銷售量的方差分別為
的值;記所抽取樣本中甲種酸奶與乙種酸奶日銷售量的方差分別為![]() ,
, ![]() ,試比較
,試比較![]() 與
與![]() 的大小(只需寫出結論);
的大小(只需寫出結論);
(Ⅱ)從甲種酸奶日銷售量在區間![]() 的數據樣本中抽取3個,記在
的數據樣本中抽取3個,記在![]() 內的數據個數為
內的數據個數為![]() ,求
,求![]() 的分布列;
的分布列;
(Ⅲ)估計1200個日銷售量數據中,數據在區間![]() 中的個數.
中的個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場舉行的“三色球”購物摸獎活動規定:在一次摸獎中,摸獎者先從裝有3個紅球與4個白球的袋中任意摸出3個球,再從裝有1個藍球與2個白球的袋中任意摸出1個球,根據摸出4個球中紅球與藍球的個數,設一、二、三等獎如下:
獎級 | 摸出紅、藍球個數 | 獲獎金額 |
一等獎 | 3紅1藍 | 200元 |
二等獎 | 3紅0藍 | 50元 |
三等獎 | 2紅1藍 | 10元 |
其余情況無獎且每次摸獎最多只能獲得一個獎級.
(1)求一次摸獎恰好摸到1個紅球的概率;
(2)求摸獎者在一次摸獎中獲獎金額X的分布列.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com