
【題目】設函數![]() (
(![]() 為自然對數的底數),
為自然對數的底數),![]() .
.
(1)證明:當![]() 時,
時, ![]() 沒有零點;
沒有零點;
(2)若當![]() 時,
時, ![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1)見解析;(2)![]()
【解析】試題分析:(1)由![]() ,令
,令![]() ,
, ![]() ,把
,把![]() 沒有零點,可以看作函數
沒有零點,可以看作函數![]() 與
與![]() 的圖象無交點,求得直線
的圖象無交點,求得直線![]() 與曲線
與曲線![]() 無交點,即可得到結論.
無交點,即可得到結論.
(2)由題意,分離參數得![]() ,設出新函數
,設出新函數![]() ,得出函數
,得出函數![]() 的單調性,求解函數
的單調性,求解函數![]() 的最小值
的最小值![]() ,即可求解
,即可求解![]() 的取值范圍.
的取值范圍.
試題解析:
(1)解法一:∵![]() ,∴
,∴![]() .
.
令![]() ,解得
,解得![]() ;令
;令![]() ,解得
,解得![]() ,
,
∴![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
∴![]() .
.
當![]() 時,
時, ![]() ,
,
∴![]() 的圖象恒在
的圖象恒在![]() 軸上方,∴
軸上方,∴![]() 沒有零點.
沒有零點.
解法二:由![]() 得
得![]() ,令
,令![]() ,
, ![]() ,
,
則![]() 沒有零點,可以看作函數
沒有零點,可以看作函數![]() 與
與![]() 的圖象無交點,
的圖象無交點,
設直線![]() 切
切![]() 于點
于點![]() ,則
,則![]() ,解得
,解得![]() ,
,
∴![]() ,代入
,代入![]() 得
得![]() ,又
,又![]() ,
,
∴直線![]() 與曲線
與曲線![]() 無交點,即
無交點,即![]() 沒有零點.
沒有零點.
(2)當![]() 時,
時, ![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]() .
.
令![]() ,則
,則![]() .
.
當![]() 時,
時, ![]() 恒成立,
恒成立,
令![]() ,解得
,解得![]() ;令
;令![]() ,解得
,解得![]() ,
,
∴![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
∴![]() .∴
.∴![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】已知a>0,a≠1且loga3>loga2,若函數f(x)=logax在區間[a,2a]上的最大值與最小值之差為1.
(1)求a的值;
(2)解不等式 ![]() ;
;
(3)求函數g(x)=|logax﹣1|的單調區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方體ABCD﹣A1B1C1D1中,M、N分別為棱C1D1、C1C的中點,有以下四個結論: ①直線AM與CC1是相交直線;
②直線AM與BN是平行直線;
③直線BN與MB1是異面直線;
④直線AM與DD1是異面直線.
其中正確的結論為(注:把你認為正確的結論的序號都填上).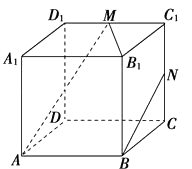
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)的定義域為R,f(x)= ![]() ,且對任意的x∈R都有f(x+1)=﹣
,且對任意的x∈R都有f(x+1)=﹣ ![]() ,若在區間[﹣5,1]上函數g(x)=f(x)﹣mx+m恰有5個不同零點,則實數m的取值范圍是( )
,若在區間[﹣5,1]上函數g(x)=f(x)﹣mx+m恰有5個不同零點,則實數m的取值范圍是( )
A.[﹣ ![]() ,﹣
,﹣ ![]() )
)
B.(﹣ ![]() ,﹣
,﹣ ![]() ]
]
C.(﹣ ![]() ,0]
,0]
D.(﹣ ![]() ,﹣
,﹣ ![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2013年第三季度,國家電網決定對城鎮居民用電計費標準作出調整,并根據用電情況將居民分為三類:第一類的用電區間在(0,170],第二類在(170,260],第三類在(260,+∞)(單位:千瓦時).某小區共有1000戶居民,現對他們的用電情況進行調查,得到頻率分布直方圖,如圖所示.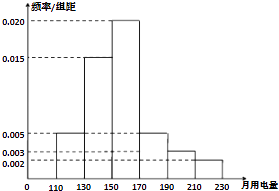
(1)求該小區居民用電量的中位數與平均數;
(2)本月份該小區沒有第三類的用電戶出現,為鼓勵居民節約用電,供電部門決定:對第一類每戶獎勵20元錢,第二類每戶獎勵5元錢,求每戶居民獲得獎勵的平均值;
(3)利用分層抽樣的方法從該小區內選出5位居民代表,若從該5戶居民代表中任選兩戶居民,求這兩戶居民用電資費屬于不同類型的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在區間D上,如果函數f(x)為減函數,而xf(x)為增函數,則稱f(x)為D上的弱減函數.若f(x)= ![]()
(1)判斷f(x)在區間[0,+∞)上是否為弱減函數;
(2)當x∈[1,3]時,不等式 ![]() 恒成立,求實數a的取值范圍;
恒成立,求實數a的取值范圍;
(3)若函數g(x)=f(x)+k|x|﹣1在[0,3]上有兩個不同的零點,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某理科考生參加自主招生面試,從7道題中(4道理科題3道文科題)不放回地依次任取3道作答.
(1)求該考生在第一次抽到理科題的條件下,第二次和第三次均抽到文科題的概率;
(2)規定理科考生需作答兩道理科題和一道文科題,該考生答對理科題的概率均為![]() ,答對文科題的概率均為
,答對文科題的概率均為![]() ,若每題答對得10分,否則得零分.現該生已抽到三道題(兩理一文),求其所得總分
,若每題答對得10分,否則得零分.現該生已抽到三道題(兩理一文),求其所得總分![]() 的分布列與數學期望
的分布列與數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知A、B、C、D為圓O上的四點,直線DE為圓O的切線,AC∥DE,AC與BD相交于H點.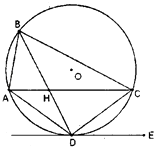
(1)求證:BD平分∠ABC;
(2)若AB=4,AD=6,BD=8,求AH的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com