
分析 (1)由已知得函數f(x)=x2(x≠0,a∈R),根據函數奇偶性的定義,可判斷出f(x)=x2為偶函數;
(2)根據f(x)在區間[2,+∞)是增函數,結合函數單調性的定義,可得當x2>x1≥2,f(x1)-f(x2)<0,由此構造關于a的不等式,解不等式可得實數a的取值范圍.
解答 解:(1)a=0時,f(x)=x2,顯然f(-x)=f(x),定義域是(-∞,0)∪(0,+∞),關于原點對稱,
故f(x)是偶函數;
(2)設x2>x1≥2,f(x1)-f(x2)=${{x}_{1}}^{2}$+$\frac{a}{{x}_{1}}$-${{x}_{2}}^{2}$-$\frac{a}{{x}_{2}}$=$\frac{{{x}_{1}-x}_{2}}{{{x}_{1}x}_{2}}$[x1x2(x1+x2)-a],
由x2>x1≥2得x1x2(x1+x2)>16,x1-x2<0,x1x2>0
要使f(x)在區間[2,+∞)是增函數只需f(x1)-f(x2)<0,
即x1x2(x1+x2)-a>0恒成立,則a≤16.
另解(導數法):f′(x)=2x-$\frac{a}{{x}^{2}}$,
要使f(x)在區間[2,+∞)是增函數,
只需當x≥2時,f'(x)≥0恒成立,即2x-$\frac{a}{{x}^{2}}$≥0,
則a≤2x3∈[16,+∞)恒成立,
故當a≤16時,f(x)在區間[2,+∞)是增函數.
點評 本題考查的知識點是函數奇偶性的性質,函數單調性的性質,熟練掌握函數奇偶性和單調性的定義,將已知轉化為關于參數a的方程(不等式)是解答本題的關鍵.


科目:高中數學 來源: 題型:選擇題
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | 1 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
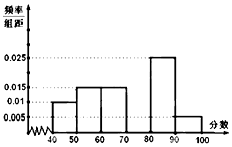 某校從參加高二年級數學競賽考試的學生中抽出60名學生,將其成績分成六段,然后畫出如圖所示部分頻率分布直方圖.觀察圖形的信息,回答下列問題:
某校從參加高二年級數學競賽考試的學生中抽出60名學生,將其成績分成六段,然后畫出如圖所示部分頻率分布直方圖.觀察圖形的信息,回答下列問題:查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{6}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com