
【題目】如圖,已知圖形ABCDEF,內部連有線段.
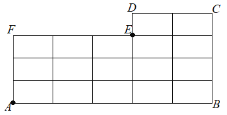
(1)由點A沿著圖中的線段到達點E的最近路線有多少條?
(2)由點A沿著圖中的線段到達點C的最近路線有多少條?
(3)求出圖中總計有多少個矩形?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由題意轉化條件為點A需向右移動3次、向上移動3次,結合組合的知識即可得解;
(2)設出直線![]() 上其它格點為
上其它格點為![]() 、
、![]() 、
、![]() ,按照
,按照![]() 、
、![]() 、
、![]() 、
、![]() 分類,結合分步乘法、組合的知識即可得解;
分類,結合分步乘法、組合的知識即可得解;
(3)由題意轉化條件為從豎線中選出兩條、橫線中選出兩條組成圖形,按照矩形的邊在不在![]() 上分類,利用分步乘法、組合的知識即可得解.
上分類,利用分步乘法、組合的知識即可得解.
(1)由題意點A沿著圖中的線段到達點E的最近路線需要移動6次:向右移動3次,向上移動3次,故點A到達點E的最近路線的條數為![]() ;
;
(2)設點![]() 、
、![]() 、
、![]() 的位置如圖所示:
的位置如圖所示:
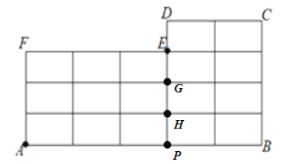
則點A沿著圖中的線段到達點C的最近路線可分為4種情況:
①沿著![]() ,共有
,共有![]() 條最近路線;
條最近路線;
②沿著![]() ,共有
,共有![]() 條最近路線;
條最近路線;
③沿著![]() ,共有
,共有![]() 條最近路線;
條最近路線;
④沿著![]() ,共有
,共有![]() 條最近路線;
條最近路線;
故由點A沿著圖中的線段到達點C的最近路線有![]() 條;
條;
(3)由題意,要組成矩形則應從豎線中選出兩條、橫線中選出兩條,可分為兩種情況:
①矩形的邊不在![]() 上,共有
上,共有![]() 個矩形;
個矩形;
②矩形的一條邊在![]() 上,共有
上,共有![]() 個矩形;
個矩形;
故圖中共有![]() 個矩形.
個矩形.


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() 的左右焦點分別為
的左右焦點分別為![]() ,
,![]() ,實軸長為6,漸近線方程為
,實軸長為6,漸近線方程為![]() ,動點
,動點![]() 在雙曲線左支上,點
在雙曲線左支上,點![]() 為圓
為圓![]() 上一點,則
上一點,則![]() 的最小值為
的最小值為
A. 8 B. 9 C. 10 D. 11
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】部分與整體以某種相似的方式呈現稱為分形.謝爾賓斯基三角形是一種分形,由波蘭數學家謝爾賓斯基1915年提出.具體操作是取一個實心三角形,沿三角形的三邊中點連線,將它分成4個小三角形,去掉中間的那一個小三角形后,對其余3個小三角形重復上述過程逐次得到各個圖形,如上圖.現在圖(3)中隨機選取一個點,則此點取自陰影部分的概率為________

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下邊的折線圖給出的是甲、乙兩只股票在某年中每月的收盤價格,已知股票甲的極差是6.88元,標準差為2.04元;股票乙的極差為27.47元,標準差為9.63元,根據這兩只股票在這一年中的波動程度,給出下列結論:①股票甲在這一年中波動相對較小,表現的更加穩定;②購買股票乙風險高但可能獲得高回報;③股票甲的走勢相對平穩,股票乙的股價波動較大;④兩只般票在全年都處于上升趨勢.其中正確結論的個數是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 離心率為
離心率為![]() ,以原點為圓心,以橢圓C的短半軸長為半徑的圓O與直線
,以原點為圓心,以橢圓C的短半軸長為半徑的圓O與直線![]() :
:![]() 相切.
相切.
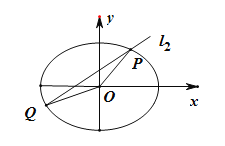
(1)求橢圓C的方程;
(2)設不過原點O的直線![]() 與該橢圓交于P、Q兩點,滿足直線OP,PQ,OQ的斜率依次成等比數列,求△OPQ面積的取值范圍.
與該橢圓交于P、Q兩點,滿足直線OP,PQ,OQ的斜率依次成等比數列,求△OPQ面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 過點
過點![]() .
.
(1)求橢圓![]() 的方程,并求其離心率;
的方程,并求其離心率;
(2)過點![]() 作
作![]() 軸的垂線
軸的垂線![]() ,設點
,設點![]() 為第四象限內一點且在橢圓
為第四象限內一點且在橢圓![]() 上(點
上(點![]() 不在直線
不在直線![]() 上),點
上),點![]() 關于
關于![]() 的對稱點為
的對稱點為![]() ,直線
,直線![]() 與
與![]() 交于另一點
交于另一點![]() .設
.設![]() 為原點,判斷直線
為原點,判斷直線![]() 與直線
與直線![]() 的位置關系,并說明理由.
的位置關系,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】沙漏是我國古代的一種計時工具,是用兩個完全相同的圓錐頂對頂疊放在一起組成的(如圖).在一個圓錐中裝滿沙子,放在上方,沙子就從頂點處漏到另一個圓錐中,假定沙子漏下來的速度是恒定的.已知一個沙漏中沙子全部從一個圓錐中漏到另一個圓錐中需用時10分鐘.那么經過5分鐘后,沙漏上方圓錐中的沙子的高度與下方圓錐中的沙子的高度之比是(假定沙堆的底面是水平的)( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,四棱錐![]() 中,
中,![]() 菱形
菱形![]() 所在的平面,
所在的平面,![]() 是
是![]() 中點,
中點,![]() 是
是![]() 上的點.
上的點.
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中點,當
的中點,當![]() 時,是否存在點
時,是否存在點![]() ,使直線
,使直線![]() 與平面
與平面![]() 的所成角的正弦值為
的所成角的正弦值為![]() ?若存在,請求出
?若存在,請求出![]() 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com