
���}Ŀ����֪���κ���(sh��)![]() ��
�� ![]() .
.
��1����![]() ����������(sh��)�Ć��{(di��o)���^(q��)�g�͜p�^(q��)�g��
����������(sh��)�Ć��{(di��o)���^(q��)�g�͜p�^(q��)�g��
��2����![]() ����(sh��)�����ֵ����Сֵ��
����(sh��)�����ֵ����Сֵ��
��3��������(sh��)��![]() ���dž��{(di��o)����(sh��)����(sh��)��(sh��)
���dž��{(di��o)����(sh��)����(sh��)��(sh��)![]() ��ȡֵ����.
��ȡֵ����.
���𰸡���1�����{(di��o)�f���^(q��)�g��![]() �����{(di��o)�f�p�^(q��)�g��
�����{(di��o)�f�p�^(q��)�g��![]() .��2����(d��ng)
.��2����(d��ng)![]() �r��
�r�� ![]() ����(d��ng)
����(d��ng)![]() �r��
�r�� ![]() .��3��
.��3��![]() ��
��![]() .
.
��������ԇ�}��������1������(j��)���κ���(sh��)���Q�S�_������(sh��)���{(di��o)�^(q��)�g��2������(j��)���Q�S�c���x�^(q��)�gλ���P(gu��n)ϵ�_������(sh��)��ֵȡ����3�����}�⌦�Q�S���څ^(q��)�g��-4,6����(n��i)����![]() ��
��![]() ���ⲻ��ʽ�Ì�(sh��)��(sh��)
���ⲻ��ʽ�Ì�(sh��)��(sh��)![]() ��ȡֵ����.
��ȡֵ����.
ԇ�}��������1����(d��ng)![]() �r��
�r�� ![]() ��
�� ![]() ��
��
����?y��n)钁�タ�_�����ϣ��������Ć��{(di��o)�f���^(q��)�g��![]() �����{(di��o)�f�p�^(q��)�g��
�����{(di��o)�f�p�^(q��)�g��![]() .
.
��2����(d��ng)![]() �r��
�r�� ![]() ��
�� ![]() ��
��
�D���_�����ϣ����Ԯ�(d��ng)![]() �r��
�r�� ![]() ����(d��ng)
����(d��ng)![]() �r��
�r�� ![]() .
.
��3��������(sh��)��![]() ���dž��{(di��o)����(sh��)���t��
���dž��{(di��o)����(sh��)���t��![]() ��֪���Č��Q�S��
��֪���Č��Q�S��![]() ��������
��������![]() �φ��{(di��o)���t
�φ��{(di��o)���t![]() ��
��![]() ����
���� ![]() ��
��![]() .
.


 ÿ��10��犿��������������쾚ϵ�д�
ÿ��10��犿��������������쾚ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����Ԫ![]() �����ң��҇���(sh��)�W(xu��)�҄��հl(f��)�F(xi��n)��(d��ng)�A��(n��i)������߅�ε�߅��(sh��)�o�����ӕr����߅�ε���e�ɟo�ޱƽ��A����e������(chu��ng)���ˡ���A�g(sh��)�����յõ��ˈA���ʾ��_��С��(sh��)�c(di��n)���λ�Ľ���ֵ
�����ң��҇���(sh��)�W(xu��)�҄��հl(f��)�F(xi��n)��(d��ng)�A��(n��i)������߅�ε�߅��(sh��)�o�����ӕr����߅�ε���e�ɟo�ޱƽ��A����e������(chu��ng)���ˡ���A�g(sh��)�����յõ��ˈA���ʾ��_��С��(sh��)�c(di��n)���λ�Ľ���ֵ![]() ���@���������ġ����ʡ�.��D�����Ä��յġ���A�g(sh��)��˼���O(sh��)Ӌ(j��)��һ�������D������
���@���������ġ����ʡ�.��D�����Ä��յġ���A�g(sh��)��˼���O(sh��)Ӌ(j��)��һ�������D������![]() ��ʾ�A��(n��i)������߅�ε�߅��(sh��)����(zh��)�д��㷨ݔ���ĈA���ʵĽ���ֵ���Ξ� �� ��
��ʾ�A��(n��i)������߅�ε�߅��(sh��)����(zh��)�д��㷨ݔ���ĈA���ʵĽ���ֵ���Ξ� �� ��
��������(sh��)��(j��)�� ![]() ��
��
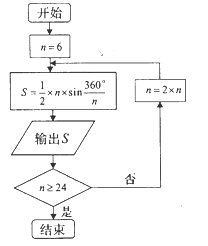
A. 2.598,3,3.1048 B. 2.598,3,3.1056
C. 2.578,3,3.1069 D. 2.588,3,3.1108
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() �鳣��(sh��)��
�鳣��(sh��)��![]() =2.71828��������Ȼ����(sh��)�ĵה�(sh��)��������
=2.71828��������Ȼ����(sh��)�ĵה�(sh��)��������![]() ���c(di��n)
���c(di��n)![]() ̎���о��c
̎���о��c![]() �Sƽ�У�
�Sƽ�У�
��1����![]() ��ֵ��
��ֵ��
��2����![]() ���{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
��3���O(sh��)![]() ������
������![]() ��
��![]() ��(d��o)����(sh��)���C����������
��(d��o)����(sh��)���C����������![]() ��0��
��0��![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��
��1��ӑՓ����(sh��)![]() �����{(di��o)�ԣ�
�����{(di��o)�ԣ�
��2����(d��ng)![]() �r��
�r��![]() ����������(sh��)��(sh��)
����������(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
��3���C����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���ڶ����wABCDEF�У�����ABCD�����Σ���߅��ADEF�������Σ�AB��DC��AB��AD��1��CD��2��AC��EC��![]() ��
��
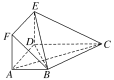
(1)���C��ƽ��EBC��ƽ��EBD��
(2)�O(sh��)M�龀��EC��һ�c(di��n)����3EM��EC��ԇ���ھ���BC���Ƿ����һ�c(di��n)T��ʹ��MT��ƽ��BDE�������ڣ�ԇָ���c(di��n)T��λ�ã��������ڣ�Ո�f�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
��1����(d��ng)![]() �r�����C��
�r�����C�� ![]() ��
��
��2����(d��ng)![]() ��
��![]() �r����(sh��)
�r����(sh��)![]() ����Сֵ��
����Сֵ��
��3����![]() ���C����
���C���� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)f��x��=4x2��4ax+a2��2a+2�څ^(q��)�g[0��2]������Сֵ3����(sh��)��(sh��)a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ������Ȼ��(sh��)![]() ��
��![]() ��
��![]() ��ǡ��һ��ż��(sh��)���r���_�ķ��O(sh��)�飨 ��
��ǡ��һ��ż��(sh��)���r���_�ķ��O(sh��)�飨 ��
A. ![]() ��
��![]() ��
��![]() �����攵(sh��) B.
�����攵(sh��) B. ![]() ��
��![]() ��
��![]() �����Ѓɂ�ż��(sh��)
�����Ѓɂ�ż��(sh��)
C. ![]() ��
��![]() ��
��![]() ����ż��(sh��) D.
����ż��(sh��) D. ![]() ��
��![]() ��
��![]() �ж����攵(sh��)�������Ѓɂ�ż��(sh��)
�ж����攵(sh��)�������Ѓɂ�ż��(sh��)
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
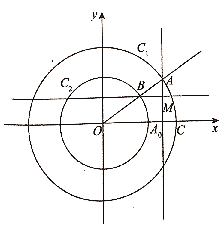
���}Ŀ����D��ʾ����ԭ�c(di��n)![]() ��A�ĵăɂ�ͬ�ĈA
��A�ĵăɂ�ͬ�ĈA![]() �����У���A
�����У���A![]() �İ돽��
�İ돽��![]() ��С�A�İ돽��
��С�A�İ돽��![]() ���c(di��n)
���c(di��n)![]() ���A
���A![]() ��һ���c(di��n)���B��
��һ���c(di��n)���B��![]() ���cС�A
���c�A![]() �����c(di��n)
�����c(di��n)![]() ���^�c(di��n)
���^�c(di��n)![]() ��
��![]() �S�Ĵ����������
�S�Ĵ����������![]() ���^�c(di��n)
���^�c(di��n)![]() ��ֱ��
��ֱ��![]() �Ĵ����������
�Ĵ����������![]() ���c(di��n)
���c(di��n)![]() ��ӛ
��ӛ![]() .
.
��1�����c(di��n)![]() ������(bi��o)���ú���
������(bi��o)���ú���![]() ��ʽ�ӱ�ʾ�����������c(di��n)
��ʽ�ӱ�ʾ�����������c(di��n)![]() ��܉�E���̣�ָ���c(di��n)
��܉�E���̣�ָ���c(di��n)![]() ��܉�E��ʲô������
��܉�E��ʲô������
��2���O(sh��)�c(di��n)![]() ��܉�E��
��܉�E��![]() ���c(di��n)
���c(di��n)![]() �քe������
�քe������![]() �ϵăɂ����c(di��n)����
�ϵăɂ����c(di��n)����![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com