對于數列{an},定義數列{an+1-an}為{an}的“差數列”.
(I)若{an}的“差數列”是一個公差不為零的等差數列,試寫出{an}的一個通項公式;
(II)若a1=2,{an}的“差數列”的通項為2n,求數列{an}的前n項和Sn;
(III)對于(II)中的數列{an},若數列{bn}滿足anbnbn+1=-21•28(n∈N*),且b4=-7.
求:①數列{bn}的通項公式;②當數列{bn}前n項的積最大時n的值.
【答案】
分析:(1)根據題意寫出符合題意的式子.
(2)依題意得{a
n}是公比數為2的等比數列,計算出數列{a
n}的前n項和S
n
(3)根據題意計算出數列{b
n}的通項公式,計算出數列{b
n}前n項的積為T
n,當數列{b
n}前n項的積最大時n的值.
解答:解:(Ⅰ)如a
n=n
2.(答案不惟一,結果應為a
n=An
2+Bn+C的形式,其中A≠0)(3分)
(Ⅱ)依題意a
n+1-a
n=2
n,n=1,2,3,
所以a
n=(a
n-a
n-1)+(a
n-1-a
n-2)+(a
n-2-a
n-3)++(a
2-a
1)+a
1=2
n-1+2
n-2+2
n-3++2=2
n.(5分)
從面{a
n}是公比數為2的等比數列,
所以
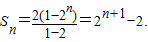
(7分)
(Ⅲ)由a
nb
nb
n+1=-21•2
n及a
n-1b
n-1b
n=-21•2
n,兩式相除得
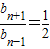
,
所以數列{b
2n-1},{b
2n}分別是公比為

的等比數列
由b
4=-7得b
2=-14.
令n=1,由a
1b
1b
2=-21•2
n得b
1=3•2
6.
所以數列{b
n}的通項為

(10分)
②記數列{b
n}前n項的積為T
n.
令

,
即
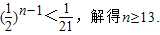
所以當n是奇數時,|b
1b
2|>1,|b
3b
4|>1,,|b
11b
12|>1,|b
13b
14|<1,|b
15b
16|<1,
從而|T
2|<|T
4|<|T
12|,|T
12|>|T
14|>.
當n是偶數時,|b
2b
3|>1,|b
4b
5|>1,,|b
12b
13|>1,|b
14b
15|<1,|b
16b
17|<1,
從而|T
1|<|T
3|<|T
13|,|T
13|>|T
15|.
注意到T
12>0,T
13>0,且T
13=b
13T
12=3T
12>T
12,
所以當數列{b
n}前n項的積T
n最大時n=13.(14分)
點評:此題主要考查數列通項公式的求解及前n項積的求解.

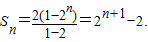 (7分)
(7分)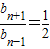 ,
, 的等比數列
的等比數列 (10分)
(10分) ,
,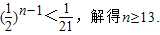


 ,數列{an}滿足an+1=H(an)(n∈N*),且a1∈(0,1),試判斷an+1與an的大小,并證明之.
,數列{an}滿足an+1=H(an)(n∈N*),且a1∈(0,1),試判斷an+1與an的大小,并證明之. ,數列{an}滿足an+1=H(an)(n∈N*),且a1∈(0,1),試判斷an+1與an的大小,并證明之.
,數列{an}滿足an+1=H(an)(n∈N*),且a1∈(0,1),試判斷an+1與an的大小,并證明之.