
【題目】如圖,四邊形ABCD為平行四邊形,點E在AB上,AE=2EB=2,且DE⊥AB.以DE為折痕把△ADE折起,使點A到達點F的位置,且∠FEB=60°.
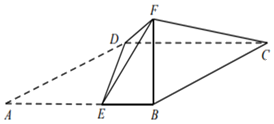
(1)求證:平面BFC⊥平面BCDE;
(2)若直線DF與平面BCDE所成角的正切值為![]() ,求二面角E﹣DF﹣C的正弦值.
,求二面角E﹣DF﹣C的正弦值.
【答案】(1)證明見解析(2)![]()
【解析】
(1)首先通過證明![]() 平面
平面![]() 證得
證得![]() .結合余弦定理和勾股定理證得
.結合余弦定理和勾股定理證得![]() ,由此證得
,由此證得![]() 平面
平面![]() ,進而證得平面
,進而證得平面![]() 平面
平面![]() .
.
(2)建立空間直角坐標系,由直線![]() 與平面
與平面![]() 所成角的正切值求得正弦值,結合直線
所成角的正切值求得正弦值,結合直線![]() 的方向向量和平面
的方向向量和平面![]() 的法向量列方程,解方程求得
的法向量列方程,解方程求得![]() 的長.由此通過平面
的長.由此通過平面![]() 和平面
和平面![]() 的法向量,計算出二面角
的法向量,計算出二面角![]() 的余弦值,進而求得其正弦值.
的余弦值,進而求得其正弦值.
(1)證明:∵DE⊥AB,∴DE⊥EB,DE⊥EF,
∴DE⊥平面BEF,∴DE⊥BF,
∵AE=2EB=2,∴EF=2,EB=1,
∵∠FEB=60°,∴由余弦定理得BF![]() ,
,
∴EF2=EB2+BF2,∴FB⊥EB,
由①②得BF⊥平面BCDE,
∴平面BFC⊥平面BCDE.
(2)解:以B為原點,BA為x軸,在平面ABCD中過點B作AB的垂線為y軸,BF為z軸,建立空間直角坐標系,
設DE=a,則D(1,a,0),F(0,0,![]() ),
),![]() (﹣1,﹣a,
(﹣1,﹣a,![]() ),
),
∵直線DF與平面BCDE所成角的正切值為![]() ,
,
∴直線DF與平面BCDE所成角的正弦值為![]() ,
,
平面BCDE的法向量![]() (0,0,1),
(0,0,1),
∴|cos![]() |
|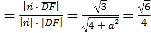 ,解得a=2,
,解得a=2,
∴D(1,2,0),C(﹣2,2,0),∴![]() (0,2,0),
(0,2,0),![]() (﹣1,﹣2,
(﹣1,﹣2,![]() ),
),
設平面EDF的法向量![]() (x,y,z),
(x,y,z),
則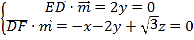 ,取z=1,得
,取z=1,得![]() (
(![]() ),
),
同理得平面DFC的一個法向量![]() (0,
(0,![]() ,2),
,2),
∴cos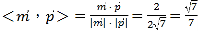 ,
,
∴二面角E﹣DF﹣C的正弦值為sin![]() .
.


科目:高中數學 來源: 題型:
【題目】為了解運動健身減肥的效果,某健身房調查了20名肥胖者,健身之前他們的體重情況如三維餅圖(1)所示,經過四個月的健身后,他們的體重情況如三維餅圖(2)所示.對比健身前后,關于這20名肥胖者,下面結論不正確的是( )
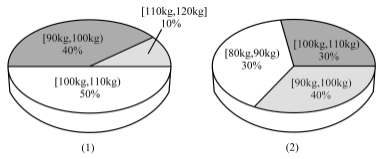
A.他們健身后,體重在區間[90kg,100kg)內的人數不變
B.他們健身后,體重在區間[100kg,110kg)內的人數減少了4人
C.他們健身后,這20位健身者體重的中位數位于[90kg,100kg)
D.他們健身后,原來體重在[110kg,120kg]內的肥胖者體重都至少減輕了10kg
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在國家“大眾創業,萬眾創新”戰略下,某企業決定加大對某種產品的研發投入.為了對新研發的產品進行合理定價,將該產品按事先擬定的價格試銷,得到一組檢測數據如表所示:
試銷價格 |
|
|
|
|
|
|
產品銷量 |
|
|
|
|
|
|
已知變量![]() 且有線性負相關關系,現有甲、乙、丙三位同學通過計算求得回歸直線方程分別為:甲
且有線性負相關關系,現有甲、乙、丙三位同學通過計算求得回歸直線方程分別為:甲![]() ; 乙
; 乙![]() ;丙
;丙![]() ,其中有且僅有一位同學的計算結果是正確的.
,其中有且僅有一位同學的計算結果是正確的.
(1)試判斷誰的計算結果正確?
(2)若由線性回歸方程得到的估計數據與檢測數據的誤差不超過![]() ,則稱該檢測數據是“理想數據”,現從檢測數據中隨機抽取
,則稱該檢測數據是“理想數據”,現從檢測數據中隨機抽取![]() 個,求“理想數據”的個數為
個,求“理想數據”的個數為![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】據歷年大學生就業統計資料顯示:某大學理工學院學生的就業去向涉及公務員、教師、金融、商貿、公司和自主創業等六大行業.2020屆該學院有數學與應用數學、計算機科學與技術和金融工程等三個本科專業,畢業生人數分別是70人,140人和210人.現采用分層抽樣的方法,從該學院畢業生中抽取18人調查學生的就業意向.
(1)應從該學院三個專業的畢業生中分別抽取多少人?
(2)國家鼓勵大學生自主創業,在抽取的18人中,含有“自主創業”就業意向的有6人,且就業意向至少有三個行業的學生有7人.為方便統計,將至少有三個行業就業意向的這7名學生分別記為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,統計如下表:
,統計如下表:
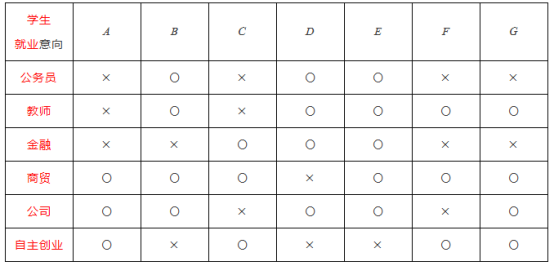
其中“○”表示有該行業就業意向,“×”表示無該行業就業意向.
①試估計該學院2020屆畢業生中有自主創業意向的學生人數;
②現從![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 這7人中隨機抽取2人接受采訪.設
這7人中隨機抽取2人接受采訪.設![]() 為事件“抽取的2人中至少有一人有自主創業意向”,求事件
為事件“抽取的2人中至少有一人有自主創業意向”,求事件![]() 發生的概率.
發生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某濕地公園內有一條河,現打算建一座橋將河兩岸的路連接起來,剖面設計圖紙如下:

其中,點![]() 為
為![]() 軸上關于原點對稱的兩點,曲線段
軸上關于原點對稱的兩點,曲線段![]() 是橋的主體,
是橋的主體,![]() 為橋頂,且曲線段
為橋頂,且曲線段![]() 在圖紙上的圖形對應函數的解析式為
在圖紙上的圖形對應函數的解析式為![]() ,曲線段
,曲線段![]() 均為開口向上的拋物線段,且
均為開口向上的拋物線段,且![]() 分別為兩拋物線的頂點,設計時要求:保持兩曲線在各銜接處(
分別為兩拋物線的頂點,設計時要求:保持兩曲線在各銜接處(![]() )的切線的斜率相等.
)的切線的斜率相等.
(1)求曲線段![]() 在圖紙上對應函數的解析式,并寫出定義域;
在圖紙上對應函數的解析式,并寫出定義域;
(2)車輛從![]() 經
經![]() 倒
倒![]() 爬坡,定義車輛上橋過程中某點
爬坡,定義車輛上橋過程中某點![]() 所需要的爬坡能力為:
所需要的爬坡能力為:![]() (該點
(該點![]() 與橋頂間的水平距離)
與橋頂間的水平距離)![]() (設計圖紙上該點處的切線的斜率),其中
(設計圖紙上該點處的切線的斜率),其中![]() 的單位:米.若該景區可提供三種類型的觀光車:①游客踏乘;②蓄電池動力;③內燃機動力.它們的爬坡能力分別為
的單位:米.若該景區可提供三種類型的觀光車:①游客踏乘;②蓄電池動力;③內燃機動力.它們的爬坡能力分別為![]() 米,
米,![]() 米,
米,![]() 米,又已知圖紙上一個單位長度表示實際長度
米,又已知圖紙上一個單位長度表示實際長度![]() 米,試問三種類型的觀光車是否都可以順利過橋?
米,試問三種類型的觀光車是否都可以順利過橋?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 中,
中,![]() ,前n項和為
,前n項和為![]() ,且
,且![]() .
.
(1)求![]() ;
;
(2)證明數列![]() 為等差數列,并寫出其通項公式;
為等差數列,并寫出其通項公式;
(3)設![]() ,試問是否存在正整數p,q(其中
,試問是否存在正整數p,q(其中![]() ),使
),使![]()
![]()
![]() 成等比數列?若存在,求出所有滿足條件的數組(p,q);若不存在,說明理由.
成等比數列?若存在,求出所有滿足條件的數組(p,q);若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】記無窮數列![]() 的前
的前![]() 項中最大值為
項中最大值為![]() ,最小值為
,最小值為![]() ,令
,令![]() ,則稱
,則稱![]() 是
是![]() “極差數列”.
“極差數列”.
(1)若![]() ,求
,求![]() 的前
的前![]() 項和;
項和;
(2)證明:![]() 的“極差數列”仍是
的“極差數列”仍是![]() ;
;
(3)求證:若數列![]() 是等差數列,則數列
是等差數列,則數列![]() 也是等差數列.
也是等差數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某搜索引擎廣告按照付費價格對搜索結果進行排名,點擊一次付費價格排名越靠前,被點擊的次數也可能會提高,已知某關鍵詞被甲、乙等多個公司競爭,其中甲、乙付費情況與每小時點擊量結果繪制成如下的折線圖.
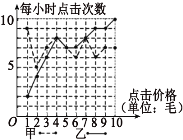
(1)若甲公司計劃從這10次競價中隨機抽取3次競價進行調研,其中每小時點擊次數超過7次的競價抽取次數記為![]() ,求
,求![]() 的分布列與數學期望;
的分布列與數學期望;
(2)若把乙公司設置的每次點擊價格為x,每小時點擊次數為![]() ,則點
,則點![]() 近似在一條直線附近.試根據前5次價格與每小時點擊次數的關系,求y關于x的回歸直線
近似在一條直線附近.試根據前5次價格與每小時點擊次數的關系,求y關于x的回歸直線![]() .(附:回歸方程系數公式:
.(附:回歸方程系數公式: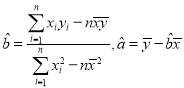
![]() ).
).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com