【題目】設f（x）=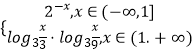 
（1）求f（log2 
）的值；
（2）求f（x）的最小值．
【答案】
（1）解：∵log2 
＜log22=1，
∴f（log2 ）= 
= 
= 
（2）解：①當x≤1時，
f（x）=2﹣x在（﹣∞，1]上是減函數，
故f（x）≥f（1）= 
；
②當x＞1時，
f（x）= 
log3 
=（log3x﹣1）（log3x﹣2）
=（log3x﹣1.5）2﹣ 
，
故當log3x=1.5時，f（x）有最小值﹣ ；
綜上所述，f（x）的最小值為﹣
【解析】（1）可判斷出log2 ＜1，從而代入分段函數求函數的值，（2）在分段函數的兩部分分別求函數的最小值，從而求分段函數的最小值即可．
【考點精析】關于本題考查的函數的最值及其幾何意義和函數的值，需要了解利用二次函數的性質（配方法）求函數的最大（小）值；利用圖象求函數的最大（小）值；利用函數單調性的判斷函數的最大（小）值；函數值的求法：①配方法(二次或四次)；②“判別式法”；③反函數法；④換元法；⑤不等式法；⑥函數的單調性法才能得出正確答案．
口算小狀元口算速算天天練系列答案科目：高中數學 來源： 題型：
【題目】甲廠根據以往的生產銷售經驗得到下面有關生產銷售的統計規律：每生產產品x（百臺），其總成本為G（x）（萬元），其中固定成本為3萬元，并且每生產1百臺的生產成本為1萬元（總成本=固定成本+生產成本），銷售收入R（x）= 
，假定該產品產銷平衡（即生產的產品都能賣掉），根據上述統計規律，請完成下列問題：
（1）寫出利潤函數y=f（x）的解析式（利潤=銷售收入﹣總成本）；
（2）甲廠生產多少臺新產品時，可使盈利最多？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知四棱錐
中，底面為矩形， 
底面
， 
， 
， 
為
上一點， 
為
的中點.
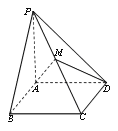
（1）在圖中作出平面
與
的交點
，并指出點
所在位置（不要求給出理由）；
（2）求平面
將四棱錐
分成上下兩部分的體積比.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給出下列四個命題：
①函數y=|x|與函數y= 
表示同一個函數；
②奇函數的圖象一定通過直角坐標系的原點；
③函數y=3（x﹣1）2的圖象可由y=3x2的圖象向右平移1個單位得到；
④若函數f（x）的定義域為[0，2]，則函數f（2x）的定義域為[0，4]；
⑤設函數f（x）是在區間[a．b]上圖象連續的函數，且f（a）f（b）＜0，則方程f（x）=0在區間[a，b]上至少有一實根．
其中正確命題的序號是 ． （填上所有正確命題的序號）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知f（x）為定義在[﹣1，1]上的奇函數，當x∈[﹣1，0]時，函數解析式f（x）= 
﹣ 
（a∈R）．
（1）寫出f（x）在[0，1]上的解析式；
（2）求f（x）在[0，1]上的最大值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
