
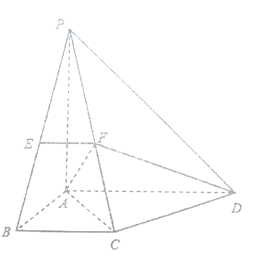
【題目】如圖,四棱錐![]() ,側面
,側面![]() 是邊長為2的正三角形,且平面
是邊長為2的正三角形,且平面![]() 平面
平面![]() ,底面
,底面![]() 是
是![]() 的菱形,
的菱形, ![]() 為棱
為棱![]() 上的動點,且
上的動點,且![]() .
.
(Ⅰ)求證: ![]() ;
;
(Ⅱ)試確定![]() 的值,使得二面角
的值,使得二面角![]() 的平面角余弦值為
的平面角余弦值為![]() .
.

【答案】(Ⅰ)證明見解析;(Ⅱ) ![]() .
.
【解析】試題分析:
(Ⅰ) 取![]() 的中點
的中點![]() ,連結
,連結![]() ,可得
,可得![]() ,
, ![]() ,從而
,從而![]() 平面
平面![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() . (Ⅱ)根據題意可得
. (Ⅱ)根據題意可得![]() 兩兩垂直,建立空間直角坐標系,求得平面
兩兩垂直,建立空間直角坐標系,求得平面![]() 和平面
和平面![]() 的法向量,根據法向量的余弦值的絕對值為
的法向量,根據法向量的余弦值的絕對值為![]() 可求得
可求得![]() ,從而可得結論.
,從而可得結論.
試題解析:
(Ⅰ)取![]() 的中點
的中點![]() ,連結
,連結![]() ,由題意可得
,由題意可得![]() ,
, ![]() 均為正三角形,
均為正三角形,
所以![]() ,
, ![]() ,
,
又![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
所以![]() .
.
因為![]() ,
,
所以![]() .
.
(Ⅱ)由(Ⅰ)可知![]() .
.
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
故可得![]() 兩兩垂直,以
兩兩垂直,以![]() 為原點,建立如圖所示的空間直角坐標系
為原點,建立如圖所示的空間直角坐標系![]() ,
,

則![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
所以 ![]() ,
,
由![]() ,可得點
,可得點![]() 的坐標為
的坐標為![]() ,
,
所以![]() ,
, ![]() ,
,
設平面![]() 的一個法向量為
的一個法向量為![]() ,
,
由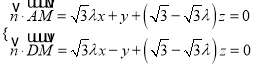 ,可得
,可得 ,
,
令![]() ,則
,則![]() ,
,
又平面![]() 的一個法向量為
的一個法向量為![]() ,
,
由題意得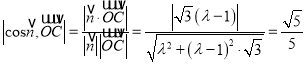 ,
,
解得![]() 或
或![]() (舍去),
(舍去),
所以當![]() 時,二面角
時,二面角![]() 的余弦值為
的余弦值為![]() .
.


 靈星計算小達人系列答案
靈星計算小達人系列答案科目:高中數學 來源: 題型:
【題目】已知△ABC的內角A, B, C的對邊分別為a, b, c,且![]() .
.
(Ⅰ)求角C的大小;
(Ⅱ)設角A的平分線交BC于D,且AD=![]() ,若b=
,若b=![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】煉鋼是一個氧化降碳的過程,鋼水含碳量的多少直接影響冶煉時間的長短,必須掌握鋼水含碳量和冶煉時間的關系.如果已測得爐料溶化完畢時鋼水的含碳量x與冶煉時間y(從爐料溶化完畢到出鋼的時間)的一組數據,如表所示:
x(0.01%) | 104 | 180 | 190 | 177 | 147 | 134 | 150 | 191 | 204 | 121 |
y/min | 100 | 200 | 210 | 185 | 155 | 135 | 170 | 205 | 235 | 125 |
(1)y與x是否具有線性相關關系?
(2)如果y與x具有線性相關關系,求回歸直線方程.
(3)預報當鋼水含碳量為160個0.01%時,應冶煉多少分鐘?
參考公式:r=![]()
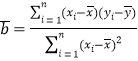 ,
,
線性回歸方程![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2018屆山西省太原十二中高三上學期1月月考】運動員甲在最近![]() 場
場![]() 比賽中所得分數的莖葉圖如圖所示,由于疏忽,莖葉圖中的兩個數據上出行了污漬,導致這兩個數字無法辨認,但統計員記得除掉污漬
比賽中所得分數的莖葉圖如圖所示,由于疏忽,莖葉圖中的兩個數據上出行了污漬,導致這兩個數字無法辨認,但統計員記得除掉污漬![]() 處的數字不影響整體中位數,且這六個數據的平均值為
處的數字不影響整體中位數,且這六個數據的平均值為![]() .
.
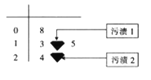
(1)求污漬![]() 處的數字;
處的數字;
(2)籃球運動員乙在最近![]() 場
場![]() 的比賽中所得分數為
的比賽中所得分數為![]() .試分別以各自
.試分別以各自![]() 場比賽得分的平均數與方差來分析這兩名籃球運動員的發揮水平.
場比賽得分的平均數與方差來分析這兩名籃球運動員的發揮水平.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,平面
中,平面![]() 平面
平面![]() ,且
,且![]() ,
,![]() .四邊形
.四邊形![]() 滿足
滿足![]() ,
,![]() ,
,![]() .
.![]() 為側棱
為側棱![]() 的中點,
的中點,![]() 為側棱
為側棱![]() 上的任意一點.
上的任意一點.
(1)若![]() 為
為![]() 的中點,求證: 面
的中點,求證: 面![]() 平面
平面![]() ;
;
(2)是否存在點![]() ,使得直線
,使得直線![]() 與平面
與平面![]() 垂直? 若存在,寫出證明過程并求出線段
垂直? 若存在,寫出證明過程并求出線段![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某花店每天以每枝5元的價格從農場購進若干枝玫瑰花,然后以每枝10元的價格出售.如果當天賣不完,剩下的玫瑰花作垃圾處理.
(1)若花店一天購進17枝玫瑰花,求當天的利潤y(單位:元)關于當天需求量n(單位:枝,n∈N)的函數解析式;
(2)花店記錄了100天玫瑰花的日需求量(單位:枝),整理得下表:
日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
頻數 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
①假設花店在這100天內每天購進17枝玫瑰花,求這100天的日利潤(單位:元)的平均數;
②若花店一天購進17枝玫瑰花,以100天記錄的各需求量的頻率作為各需求量發生的概率,求當天的利潤不少于75元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() .
.
(Ⅰ)求曲線![]() 在點
在點![]() 處的切線的斜率;
處的切線的斜率;
(Ⅱ)判斷方程![]() (
(![]() 為
為![]() 的導數)在區間
的導數)在區間![]() 內的根的個數,說明理由;
內的根的個數,說明理由;
(Ⅲ)若函數![]() 在區間
在區間![]() 內有且只有一個極值點,求
內有且只有一個極值點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com