
【題目】![]() 在直角坐標系xOy中,曲線C1:
在直角坐標系xOy中,曲線C1:![]() (t為參數,且t≠0),其中0
(t為參數,且t≠0),其中0![]()
![]()
![]() , 在以O為極點x軸正半軸為極軸的極坐標系中,曲線C2::
, 在以O為極點x軸正半軸為極軸的極坐標系中,曲線C2::![]() =2sin
=2sin![]() , C3:
, C3:![]() =2
=2![]() cos
cos![]()
(1)求C2與C3交點的直角坐標
(2)若C1與C2相交于點A,C1與C3相交于點B,求|AB|最大值
【答案】
(1)
(0.0) (![]() ,
,![]() )
)
(2)
4
【解析】(1)曲線C2的直角坐標方程為x2+y2-2y=0,曲線C3 的直角坐標方程分別為x2+y2-2![]() x=0,聯立兩方程組解可得
x=0,聯立兩方程組解可得![]() 或
或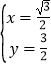 , 所以C2與C3得交點直角坐標為(0.0) (
, 所以C2與C3得交點直角坐標為(0.0) (![]() ,
,![]() )。
)。
(2)曲線C1極坐標方程為![]() =
=![]() (
(![]()
![]() R,
R,![]() ≠0),其中0
≠0),其中0![]()
![]()
![]() , 因此點A的極坐標為(2sin
, 因此點A的極坐標為(2sin![]() ,
, ![]() ),點B的極坐標為 (2
),點B的極坐標為 (2![]() cos
cos![]() ,
, ![]() ),所以|AB|=|2sin
),所以|AB|=|2sin![]() -2
-2![]() cos
cos![]() |=4|sin(
|=4|sin(![]() -
-![]() )|,當
)|,當![]() =
=![]() 時,|AB|取得最大值,最大值為4。
時,|AB|取得最大值,最大值為4。
【考點精析】根據題目的已知條件,利用參數方程的定義的相關知識可以得到問題的答案,需要掌握在平面直角坐標系中,如果曲線上任意一點的坐標![]() 都是某個變數
都是某個變數![]() 的函數
的函數![]() 并且對于
并且對于![]() 的每一個允許值,由這個方程所確定的點
的每一個允許值,由這個方程所確定的點![]() 都在這條曲線上,那么這個方程就叫做這條曲線的參數方程.
都在這條曲線上,那么這個方程就叫做這條曲線的參數方程.


科目:高中數學 來源: 題型:
【題目】如圖,某生態園將一塊三角形地ABC的一角APQ開辟為水果園,已知角A為120°,AB,AC的長度均大于200米,現在邊界AP,AQ處建圍墻,在PQ處圍竹籬笆. 
(1)若圍墻AP、AQ總長度為200米,如何可使得三角形地塊APQ面積最大?
(2)已知竹籬笆長為 ![]() 米,AP段圍墻高1米,AQ段圍墻高2米,造價均為每平方米100元,求圍墻總造價的取值范圍.
米,AP段圍墻高1米,AQ段圍墻高2米,造價均為每平方米100元,求圍墻總造價的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() 的左右焦點與其短軸的一個端點是正三角形的三個頂點,點D
的左右焦點與其短軸的一個端點是正三角形的三個頂點,點D ![]() 在橢圓C上,直線l:y=kx+m與橢圓C相交于A、P兩點,與x軸、y軸分別相交于點N和M,且PM=MN,點Q是點P關于x軸的對稱點,QM的延長線交橢圓于點B,過點A、B分別作x軸的垂涎,垂足分別為A1、B1
在橢圓C上,直線l:y=kx+m與橢圓C相交于A、P兩點,與x軸、y軸分別相交于點N和M,且PM=MN,點Q是點P關于x軸的對稱點,QM的延長線交橢圓于點B,過點A、B分別作x軸的垂涎,垂足分別為A1、B1
(1)求橢圓C的方程;
(2)是否存在直線l,使得點N平分線段A1B1?若存在,求求出直線l的方程,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題:“若![]() ,則關于x的不等式
,則關于x的不等式![]() 的解集為空集”,那么它的逆命題,否命題,逆否命題,以及原命題中,假命題的個數是( )
的解集為空集”,那么它的逆命題,否命題,逆否命題,以及原命題中,假命題的個數是( )
A.0B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于非空實數集A,定義![]() 對任意
對任意![]() .設非空實數集
.設非空實數集![]() .現給出以下命題:(1)對于任意給定符合題設條件的集合C,D,必有
.現給出以下命題:(1)對于任意給定符合題設條件的集合C,D,必有![]() ;(2)對于任意給定符合題設條件的集合C,D,必有
;(2)對于任意給定符合題設條件的集合C,D,必有![]() ;(3)對于任意給定符合題設條件的集合C,D,必有
;(3)對于任意給定符合題設條件的集合C,D,必有![]() ;(4)對于任意給定符合題設條件的集合C,D,必存在常數a,使得對任意的
;(4)對于任意給定符合題設條件的集合C,D,必存在常數a,使得對任意的![]() ,恒有
,恒有![]() .以上命題正確的個數是( )
.以上命題正確的個數是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學用“五點法”畫函數![]() 在某一周期內的圖像時,列表并填入的部分數據如下表:
在某一周期內的圖像時,列表并填入的部分數據如下表:
|
|
|
|
|
|
| 0 |
|
|
|
|
| 0 | 1 | 0 |
| 0 |
| 0 |
| 0 |
| 0 |
(1)請寫出上表的![]() 及函數
及函數![]() 的解析式;
的解析式;
(2)將函數![]() 的圖像向右平移
的圖像向右平移![]() 個單位,再將所得圖像上各點的橫坐標縮小為原來的
個單位,再將所得圖像上各點的橫坐標縮小為原來的![]() ,縱坐標不變,得到函數
,縱坐標不變,得到函數![]() 的圖像,求
的圖像,求![]() 的解析式及
的解析式及 的單調遞增區間;
的單調遞增區間;
(3)在(2)的條件下,若![]() 在
在![]() 上恰有奇數個零點,求實數
上恰有奇數個零點,求實數![]() 與零點個數
與零點個數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了調查甲、乙兩個網站受歡迎的程度,隨機選取了14天,統計上午8:00—10:00間各自的點擊量,得如下所示的統計圖,根據統計圖:

(1)甲、乙兩個網站點擊量的極差分別是多少?
(2)甲網站點擊量在[10,60]間的頻率是多少?
(3)甲、乙兩個網站哪個更受歡迎?并說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C1:x2=4y 的焦點F也是橢圓c2:![]() 的一個焦點, C1和C2的公共弦長為
的一個焦點, C1和C2的公共弦長為![]()
(1)求 C2的方程;
(2)過點F 的直線 l與 C1相交于A與B兩點, 與C2相交于C , D兩點,且![]() 與
與![]() 同向
同向
(ⅰ)若 ![]() 求直線l的斜率;
求直線l的斜率;
(ⅱ)設 C1在點 A處的切線與 x軸的交點為M ,證明:直線l 繞點 F旋轉時, ![]() MFD總是鈍角三角形。
MFD總是鈍角三角形。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2015·江蘇)如圖,在平面直角坐標系xOy中,已知橢圓![]() (a>b>0)的離心率為
(a>b>0)的離心率為![]() ,且右焦點F到左準線l的距離為3.
,且右焦點F到左準線l的距離為3.
(1)求橢圓的標準方程;
(2)過F的直線與橢圓交于A , B兩點,線段AB的垂直平分線分別交直線l和AB于 點P , C , 若PC=2AB , 求直線AB的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com