
【題目】已知y=f(x)是定義在(-∞,+∞)上的奇函數(shù),且在[0,+∞)上為增函數(shù),
(1)求證:函數(shù)在(-∞,0)上也是增函數(shù);
(2)如果f(![]() )=1,解不等式-1<f(2x+1)≤0.
)=1,解不等式-1<f(2x+1)≤0.
【答案】(1)證明見(jiàn)解析;(2){x|-![]() <x≤-
<x≤-![]() }.
}.
【解析】
(1)設(shè)![]() ,且
,且![]() ,根據(jù)單調(diào)性的定義,結(jié)合函數(shù)奇偶性,即可得證;
,根據(jù)單調(diào)性的定義,結(jié)合函數(shù)奇偶性,即可得證;
(2)根據(jù)![]() 是R上的奇函數(shù),把
是R上的奇函數(shù),把![]() ,轉(zhuǎn)化為
,轉(zhuǎn)化為![]() ,再結(jié)合函數(shù)的單調(diào)性,得到
,再結(jié)合函數(shù)的單調(diào)性,得到![]() ,即可求解.
,即可求解.
(1)設(shè)x1、x2是(-∞,0]上任意兩個(gè)不相等的實(shí)數(shù),且x1<x2,
則-x1,-x2∈[0,+∞),且-x1>-x2,Δx=x2-x1>0,Δy=f(x2)-f(x1).
因?yàn)?/span>f(x)是奇函數(shù),且在[0,+∞)上是增函數(shù),-x1>-x2,
所以f(-x1)>f(-x2).
又因?yàn)?/span>f(x)為奇函數(shù),所以f(-x1)=-f(x1),f(-x2)=-f(x2),
所以-f(x1)>-f(x2),即f(x1)<f(x2),
即Δy=f(x2)-f(x1)>0,
所以函數(shù)f(x)在(-∞,0]上也是增函數(shù).
(2)因?yàn)?/span>f(x)是R上的奇函數(shù),所以f(0)=0,f(-![]() )=-f(
)=-f(![]() )=-1,
)=-1,
由-1<f(2x+1)≤0,得f(-![]() )<f(2x+1)≤f(0).
)<f(2x+1)≤f(0).
又因?yàn)?/span>f(x)在(-∞,0)上是增函數(shù),所以-![]() <2x+1≤0,解得-
<2x+1≤0,解得-![]() <x≤-
<x≤-![]() ,
,
所以不等式的解集為{x|-![]() <x≤-
<x≤-![]() }.
}.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知曲線(xiàn)C:x2-y2=1及直線(xiàn)l:y=kx-1.
(1)若l與C有兩個(gè)不同的交點(diǎn),求實(shí)數(shù)k的取值范圍;
(2)若l與C交于A,B兩點(diǎn),O為坐標(biāo)原點(diǎn),且△AOB的面積為![]() ,求實(shí)數(shù)k的值.
,求實(shí)數(shù)k的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() (其中
(其中![]() ).
).
(1)當(dāng)![]() 時(shí),判斷
時(shí),判斷![]() 零點(diǎn)的個(gè)數(shù)k;
零點(diǎn)的個(gè)數(shù)k;
(2)在(1)的條件下,記這些零點(diǎn)分別為![]() ,求證:
,求證: ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】計(jì)劃在某水庫(kù)建一座至多安裝3臺(tái)發(fā)電機(jī)的水電站,過(guò)去50年的水文資料顯示,水庫(kù)年入流量![]() (年入流量:一年內(nèi)上游來(lái)水與庫(kù)區(qū)降水之和.單位:億立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超過(guò)120的年份有35年,超過(guò)120的年份有5年.將年入流量在以上三段的頻率作為相應(yīng)段的概率,并假設(shè)各年的年入流量相互獨(dú)立.
(年入流量:一年內(nèi)上游來(lái)水與庫(kù)區(qū)降水之和.單位:億立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超過(guò)120的年份有35年,超過(guò)120的年份有5年.將年入流量在以上三段的頻率作為相應(yīng)段的概率,并假設(shè)各年的年入流量相互獨(dú)立.
(1)求未來(lái)4年中,至多1年的年入流量超過(guò)120的概率;
(2)水電站希望安裝的發(fā)電機(jī)盡可能運(yùn)行,但每年發(fā)電機(jī)最多可運(yùn)行臺(tái)數(shù)受年入流量![]() 限制,并有如下關(guān)系:
限制,并有如下關(guān)系:
年入流量 |
|
|
|
發(fā)電量最多可運(yùn)行臺(tái)數(shù) | 1 | 2 | 3 |
若某臺(tái)發(fā)電機(jī)運(yùn)行,則該臺(tái)年利潤(rùn)為5000萬(wàn)元;若某臺(tái)發(fā)電機(jī)未運(yùn)行,則該臺(tái)年虧損800萬(wàn)元,欲使水電站年總利潤(rùn)的均值達(dá)到最大,應(yīng)安裝發(fā)電機(jī)多少臺(tái)?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】“大眾創(chuàng)業(yè),萬(wàn)眾創(chuàng)新”是李克強(qiáng)總理在本屆政府工作報(bào)告中向全國(guó)人民發(fā)出的口號(hào).某生產(chǎn)企業(yè)積極響應(yīng)號(hào)召,大力研發(fā)新產(chǎn)品,為了對(duì)新研發(fā)的一批產(chǎn)品進(jìn)行合理定價(jià),將該產(chǎn)品按事先擬定的價(jià)格進(jìn)行試銷(xiāo),得到一組銷(xiāo)售數(shù)據(jù)![]() (
(![]() =1,2,…,6),如表所示:
=1,2,…,6),如表所示:
試銷(xiāo)單價(jià) | 4 | 5 | 6 | 7 | 8 | 9 |
產(chǎn)品銷(xiāo)量 | q | 84 | 83 | 80 | 75 | 68 |
已知![]() .
.
(Ⅰ)求出![]() 的值;
的值;
(Ⅱ)已知變量![]() 具有線(xiàn)性相關(guān)關(guān)系,求產(chǎn)品銷(xiāo)量
具有線(xiàn)性相關(guān)關(guān)系,求產(chǎn)品銷(xiāo)量![]() (件)關(guān)于試銷(xiāo)單價(jià)
(件)關(guān)于試銷(xiāo)單價(jià)![]() (元)的線(xiàn)性回歸方程
(元)的線(xiàn)性回歸方程![]() ;
;
(參考公式:線(xiàn)性回歸方程中![]() ,
,![]() 的最小二乘估計(jì)分別為
的最小二乘估計(jì)分別為 ,
,![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓C:![]() (a>b>0)的兩個(gè)焦點(diǎn)分別為F1,F2,離心率為
(a>b>0)的兩個(gè)焦點(diǎn)分別為F1,F2,離心率為![]() ,過(guò)F1的直線(xiàn)l與橢圓C交于M,N兩點(diǎn),且△MNF2的周長(zhǎng)為8.
,過(guò)F1的直線(xiàn)l與橢圓C交于M,N兩點(diǎn),且△MNF2的周長(zhǎng)為8.
(1)求橢圓C的方程;
(2)若直線(xiàn)y=kx+b與橢圓C分別交于A,B兩點(diǎn),且OA⊥OB,試問(wèn)點(diǎn)O到直線(xiàn)AB的距離是否為定值,證明你的結(jié)論.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】據(jù)調(diào)查顯示,某高校![]() 萬(wàn)男生的身高服從正態(tài)分布
萬(wàn)男生的身高服從正態(tài)分布![]() ,現(xiàn)從該校男生中隨機(jī)抽取
,現(xiàn)從該校男生中隨機(jī)抽取![]() 名進(jìn)行身高測(cè)量,將測(cè)量結(jié)果分成
名進(jìn)行身高測(cè)量,將測(cè)量結(jié)果分成![]() 組:
組: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,并繪制成如圖所示的頻率分布直方圖.
,并繪制成如圖所示的頻率分布直方圖.
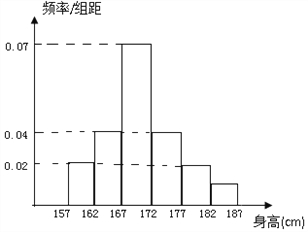
(Ⅰ)求這![]() 名男生中身高在
名男生中身高在![]() (含
(含![]() )以上的人數(shù);
)以上的人數(shù);
(Ⅱ)從這![]() 名男生中身高在
名男生中身高在![]() 以上(含
以上(含![]() )的人中任意抽取
)的人中任意抽取![]() 人,該
人,該![]() 人中身高排名(從高到低)在全校前
人中身高排名(從高到低)在全校前![]() 名的人數(shù)記為
名的人數(shù)記為![]() ,求
,求![]() 的數(shù)學(xué)期望.
的數(shù)學(xué)期望.
(附:參考數(shù)據(jù):若![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,則
,則![]() ,
, ![]() ,
, ![]() .)
.)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某超市計(jì)劃銷(xiāo)售某種食品,現(xiàn)邀請(qǐng)甲、乙兩個(gè)商家進(jìn)場(chǎng)試銷(xiāo)10天.兩個(gè)商家提供的返利方案如下:甲商家每天固定返利60元,且每賣(mài)出一件食品商家再返利3元;乙商家無(wú)固定返利,賣(mài)出30件以?xún)?nèi)(含30件)的食品,每件食品商家返利5元,超出30件的部分每件返利8元.經(jīng)統(tǒng)計(jì),兩個(gè)商家的試銷(xiāo)情況莖葉圖如下:
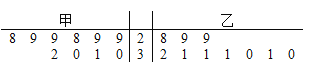
(1)現(xiàn)從甲商家試銷(xiāo)的10天中抽取兩天,求這兩天的銷(xiāo)售量都小于30的概率;
(2)若將頻率視作概率,回答以下問(wèn)題:
① 記商家乙的日返利額為X(單位:元),求X的分布列和數(shù)學(xué)期望;
② 超市擬在甲、乙兩個(gè)商家中選擇一家長(zhǎng)期銷(xiāo)售,如果僅從日平均返利額的角度考慮,請(qǐng)利用所學(xué)的統(tǒng)計(jì)學(xué)知識(shí)為超市作出選擇,并說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】![]() 年春節(jié)期間,某服裝超市舉辦了一次有獎(jiǎng)促銷(xiāo)活動(dòng),消費(fèi)每超過(guò)
年春節(jié)期間,某服裝超市舉辦了一次有獎(jiǎng)促銷(xiāo)活動(dòng),消費(fèi)每超過(guò)![]() 元(含
元(含![]() 元),均可抽獎(jiǎng)一次,抽獎(jiǎng)方案有兩種,顧客只能選擇其中的一種.方案一:從裝有
元),均可抽獎(jiǎng)一次,抽獎(jiǎng)方案有兩種,顧客只能選擇其中的一種.方案一:從裝有![]() 個(gè)形狀、大小完全相同的小球(其中紅球
個(gè)形狀、大小完全相同的小球(其中紅球![]() 個(gè),黑球
個(gè),黑球![]() 個(gè))的抽獎(jiǎng)盒中,一次性摸出
個(gè))的抽獎(jiǎng)盒中,一次性摸出![]() 個(gè)球,其中獎(jiǎng)規(guī)則為:若摸到
個(gè)球,其中獎(jiǎng)規(guī)則為:若摸到![]() 個(gè)紅球,享受免單優(yōu)惠;若摸出
個(gè)紅球,享受免單優(yōu)惠;若摸出![]() 個(gè)紅球則打
個(gè)紅球則打![]() 折,若摸出
折,若摸出![]() 個(gè)紅球,則打
個(gè)紅球,則打![]() 折;若沒(méi)摸出紅球,則不打折.方案二:從裝有
折;若沒(méi)摸出紅球,則不打折.方案二:從裝有![]() 個(gè)形狀、大小完全相同的小球(其中紅球
個(gè)形狀、大小完全相同的小球(其中紅球![]() 個(gè),黑球
個(gè),黑球![]() 個(gè))的抽獎(jiǎng)盒中,有放回每次摸取
個(gè))的抽獎(jiǎng)盒中,有放回每次摸取![]() 球,連摸
球,連摸![]() 次,每摸到
次,每摸到![]() 次紅球,立減
次紅球,立減![]() 元.
元.
(1)若兩個(gè)顧客均分別消費(fèi)了![]() 元,且均選擇抽獎(jiǎng)方案一,試求兩位顧客均享受免單優(yōu)惠的概率;
元,且均選擇抽獎(jiǎng)方案一,試求兩位顧客均享受免單優(yōu)惠的概率;
(2)若某顧客消費(fèi)恰好滿(mǎn)![]() 元,試從概率的角度比較該顧客選擇哪一種抽獎(jiǎng)方案更合算?
元,試從概率的角度比較該顧客選擇哪一種抽獎(jiǎng)方案更合算?
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com