
已知函數f(x)=aex,g(x)=lnx-lna,其中a為常數, e=2.718…,且函數y=f(x)和y=g(x)的圖像在它們與坐標軸交點處的切線互相平行.
(1)求常數a的值;
(2)若存在x使不等式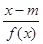 >
>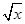 成立,求實數m的取值范圍;
成立,求實數m的取值范圍;
(3)對于函數y=f(x)和y=g(x)公共定義域內的任意實數x0,我們把|f(x0)-g(x0)|的值稱為兩函數在x0處的偏差.求證:函數y=f(x)和y=g(x)在其公共定義域內的所有偏差都大于2.
(1)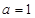 ;(2)
;(2)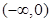 ;(3)參考解析
;(3)參考解析
解析試題分析:(1)依題意可得函數與坐標軸的交點通過求導函數即在兩坐標軸的交點的切線的斜率相等即可求出 的值.
的值.
(2)不等式恒成立的問題轉化為函數的最值問題.在對函數求導求出在定義域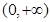 上的單調性即可求出m的取值范圍.
上的單調性即可求出m的取值范圍.
(3)本小題是把不等式的問題轉化為一個新的函數的最問題. 由于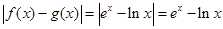 .對該函數直接研究存在困難.求導后不能得到所需要的結論.所以構造新函數
.對該函數直接研究存在困難.求導后不能得到所需要的結論.所以構造新函數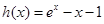 從而得到
從而得到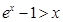 .再構造一個函數
.再構造一個函數 得到lnx+1<x.從而得到偏差要大于2的結論.本小題的解法較特殊.構造兩個函數額是解題的關鍵和突破口,同時既有創新思維.
得到lnx+1<x.從而得到偏差要大于2的結論.本小題的解法較特殊.構造兩個函數額是解題的關鍵和突破口,同時既有創新思維.
試題解析:(1)f(x)與坐標軸的交點為(0, ).
).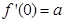 . g(x)與坐標軸的交點為(
. g(x)與坐標軸的交點為( ,0).
,0).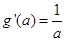 .所以
.所以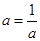 .所以
.所以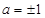 .又因為
.又因為 >0.所以
>0.所以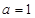 .
.
(2)因為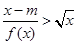 可化為
可化為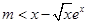 .令
.令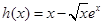 .則
.則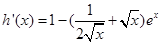 .因為x>0.所以
.因為x>0.所以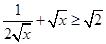 .
.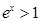 .所以
.所以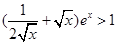 .故
.故 .所以
.所以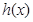 在
在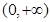 上是減函數.因此
上是減函數.因此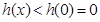 .所以實數m的取值范圍是
.所以實數m的取值范圍是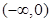 .
.
(3)y=f(x)與y=g(x)的公共定義域為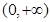 .
.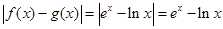 .令
.令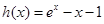 .則
.則 >0.所以h(x)在
>0.所以h(x)在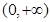 上是增函數.故h(x)>h(0)=0.即
上是增函數.故h(x)>h(0)=0.即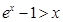 …①.令
…①.令 .則
.則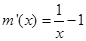 .當x>1.時.
.當x>1.時. 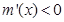 .當0<x<1時.
.當0<x<1時. 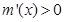 .所以m(x)有最大值m(1)=0.因此lnx+1<x…②.由①②得
.所以m(x)有最大值m(1)=0.因此lnx+1<x…②.由①②得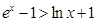 .即
.即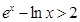 .所以函數y=f(x)和y=g(x)在其公共定義域內的所有偏差都大于2.
.所以函數y=f(x)和y=g(x)在其公共定義域內的所有偏差都大于2.
考點:1.導數的幾何意義.2.不等式轉化為恒成立問題.3.函數的構造.


科目:高中數學 來源: 題型:解答題
在實數集R上定義運算: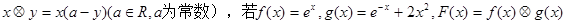
(Ⅰ)求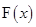 的解析式;
的解析式;
(Ⅱ)若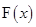 在R上是減函數,求實數a的取值范圍;
在R上是減函數,求實數a的取值范圍;
(Ⅲ)若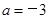 ,在
,在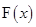 的曲線上是否存在兩點,使得過這兩點的切線互相垂直?若存在,求出切線方程;若不存在,說明理由.
的曲線上是否存在兩點,使得過這兩點的切線互相垂直?若存在,求出切線方程;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com