
在如圖所示的多面體ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,G為AD中點.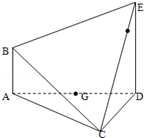
(1)請在線段CE上找到點F的位置,使得恰有直線BF∥平面ACD,并證明這一事實;
(2)求平面BCE與平面ACD所成銳二面角的大小;
(3)求點G到平面BCE的距離.
(1)點F應是線段CE的中點(2)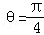 (3)
(3)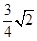
解析試題分析:解法一:以D點為原點建立如圖所示的空間直角坐標系,使得x軸和z軸的正半軸分別經過點A和點E,則各點的坐標為D(0,0,0),A(2,0,0),E(0,0,2),
B(2,0,1), ,
,
(1)點F應是線段CE的中點,下面證明:
設F是線段CE的中點,則點F的坐標為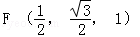 ,
,
∴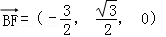 ,取平面ACD的法向量
,取平面ACD的法向量 ,
,
則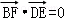 ,∴BF∥平面ACD;
,∴BF∥平面ACD;
(2)設平面BCE的法向量為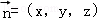 ,則
,則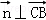 ,且
,且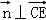 ,
,
由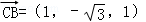 ,
, ,
,
∴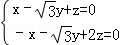 ,不妨設
,不妨設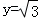 ,則
,則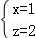 ,即
,即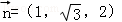 ,
,
∴所求角θ滿足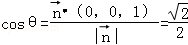 ,∴
,∴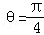 ;
;
(3)由已知G點坐標為(1,0,0),∴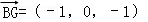 ,
,
由(2)平面BCE的法向量為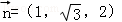 ,∴所求距離
,∴所求距離 .
.
解法二:(1)由已知AB⊥平面ACD,DE⊥平面ACD,∴AB∥ED,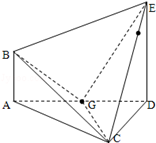
設F為線段CE的中點,H是線段CD的中點,連接FH,則FH∥=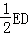 ,
,
∴FH∥=AB,∴四邊形ABFH是平行四邊形,∴BF∥AH,
由BF?平面ACD內,AH?平面ACD,∴BF∥平面ACD;
(2)由已知條件可知△ACD即為△BCE在平面ACD上的射影,
設所求的二面角的大小為θ,則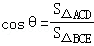 ,
,
易求得BC=BE= ,CE=
,CE= ,∴
,∴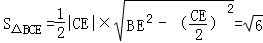 ,
,
而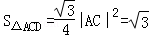 ,∴
,∴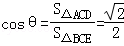 ,而
,而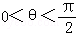 ,∴
,∴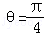 ;
;
(3)連接BG、CG、EG,得三棱錐C﹣BGE,由ED⊥平面ACD,∴平面ABED⊥平面ACD,又CG⊥AD,∴CG⊥平面ABED,設G點到平面BCE的距離為h,則VC﹣BGE=VG﹣BCE即 ,由
,由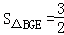 ,
,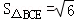 ,
,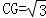 ,
,
∴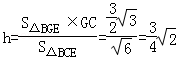 即為點G到平面BCE的距離.
即為點G到平面BCE的距離.
考點:空間幾何體線面平行的判定二面角點面距的計算
點評:當已知條件中出現了從同一點出發的三線兩兩垂直或可以平移為三線兩兩垂直時,常利用空間向量求解,只需寫出各點坐標代入相應公式即可


科目:高中數學 來源: 題型:解答題
本題共有2個小題,第(1)小題滿分6分,第(2)小題滿分6分.
如圖,已知正四棱柱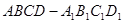 的底面邊長是
的底面邊長是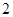 ,體積是
,體積是 ,
, 分別是棱
分別是棱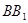 、
、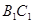 的中點.
的中點.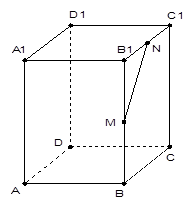
(1)求直線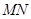 與平面
與平面 所成的角(結果用反三角函數表示);
所成的角(結果用反三角函數表示);
(2)求過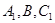 的平面與該正四棱柱所截得的多面體
的平面與該正四棱柱所截得的多面體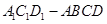 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知四棱柱 的底面是邊長為1的正方形,側棱垂直底邊ABCD四棱柱,
的底面是邊長為1的正方形,側棱垂直底邊ABCD四棱柱, ,
,
E是側棱AA1的中點,求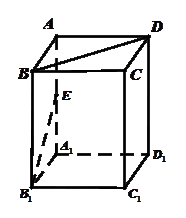
(1)求異面直線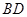 與B1E所成角的大小;
與B1E所成角的大小;
(2)求四面體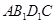 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)如圖,直角梯形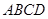 與等腰直角三角形
與等腰直角三角形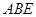 所在的平面互相垂直.
所在的平面互相垂直.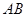 ∥
∥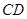 ,
,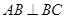 ,
, ,
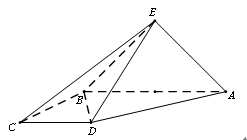
, .
.
(1)求直線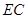 與平面
與平面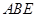 所成角的正弦值;
所成角的正弦值;
(2)線段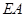 上是否存在點
上是否存在點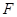 ,使
,使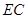 // 平面
// 平面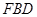 ?若存在,求出
?若存在,求出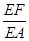 ;若不存在,說明理由.1
;若不存在,說明理由.1
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2。將△ABD沿邊AB折起, 使得△ABD與△ABC成直二面角 ,如圖二,在二面角
,如圖二,在二面角 中.
中.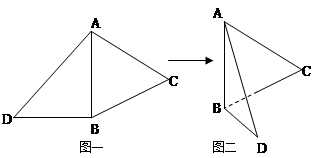
(1)求證:BD⊥AC;
(2)求D、C之間的距離;
(3)求DC與面ABD成的角的正弦值。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,正方形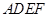 與梯形
與梯形 所在的平面互相垂直,
所在的平面互相垂直,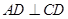 ,
, ∥
∥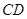 ,
,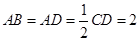 ,點
,點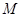 在線段
在線段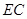 上.
上.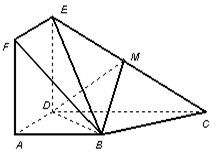
(I)當點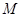 為
為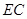 中點時,求證:
中點時,求證: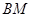 ∥平面
∥平面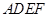 ;
;
(II)當平面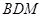 與平面
與平面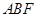 所成銳二面角的余弦值為
所成銳二面角的余弦值為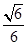 時,求三棱錐
時,求三棱錐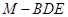 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,三棱錐P-ABC中,PC 平面ABC,PC=AC=2, AB=BC,D是PB上一點,且CD
平面ABC,PC=AC=2, AB=BC,D是PB上一點,且CD 平面PAB
平面PAB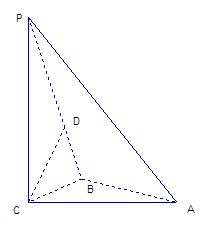
(1)求證:AB 平面PCB;
平面PCB;
(2)求異面直線AP與BC所成角的大小;
(3)求二面角C-PA-B 的大小的余弦值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com