
【題目】已知函數f(x)=![]() -x2+ef′(
-x2+ef′(![]() )x.
)x.
(Ⅰ)求f(x)的單調區間;
(Ⅱ)若存在x1,x2(x1<x2),使得f(x1)+f(x2)=1,求證:x1+x2<2.
【答案】(Ⅰ)在R上單調遞增;(Ⅱ)見解析
【解析】
(I)f′(x)=e2(x-1)-2x+ef′(![]() ).令x=
).令x=![]() ,則f′(
,則f′(![]() )=
)=![]() -1+ef′(
-1+ef′(![]() ),解得f′(
),解得f′(![]() ),進而得出函數f(x)的單調性.
),進而得出函數f(x)的單調性.
(II)由(I)可得:函數f(x))=![]() -x2+x在R上單調遞增.要證明:x1+x2<2x1<2-x2f(x1)<f(2-x2),又f(x1)+f(x2)=1,因此f(x1)<f(2-x2)1-f(x2)<f(2-x2),即f(x2)+f(2-x2)-1>0,f(1)=
-x2+x在R上單調遞增.要證明:x1+x2<2x1<2-x2f(x1)<f(2-x2),又f(x1)+f(x2)=1,因此f(x1)<f(2-x2)1-f(x2)<f(2-x2),即f(x2)+f(2-x2)-1>0,f(1)=![]() -1+1=
-1+1=![]() ,則x1<1<x2.令g(x)=f(2-x)+f(x)-1=
,則x1<1<x2.令g(x)=f(2-x)+f(x)-1=![]() +
+![]() -2x2+4x-2,x>1,g(1)=0.利用導數研究其單調性即可證明結論.
-2x2+4x-2,x>1,g(1)=0.利用導數研究其單調性即可證明結論.
(I)f′(x)=e2(x-1)-2x+ef′(![]() ).
).
令x=![]() ,則f′(
,則f′(![]() )=
)=![]() -1+ef′(
-1+ef′(![]() ),解得f′(
),解得f′(![]() )=
)=![]() .
.
∴f′(x)=e2(x-1)-2x+1.f″(x)=2e2(x-1)-2=2(ex-1+1)(ex-1-1),
![]() 時
時![]() 單調遞增;
單調遞增;![]() 時
時![]() 單調遞減,
單調遞減,
∴x=1時,函數f′(x)取得極小值即最小值,∴f′(x)≥f′(1)=0,
∴函數f(x)在R上單調遞增.
(II)由(I)可得:函數f(x)=![]() -x2+x在R上單調遞增.
-x2+x在R上單調遞增.
要證明:x1+x2<2x1<2-x2f(x1)<f(2-x2),
又f(x1)+f(x2)=1,因此f(x1)<f(2-x2)1-f(x2)<f(2-x2),
即f(x2)+f(2-x2)-1>0,f(1)=![]() =
=![]() ,則x1<1<x2.
,則x1<1<x2.
令g(x)=f(2-x)+f(x)-1=![]() -(2-x)2+2-x+
-(2-x)2+2-x+![]() -x2+x=
-x2+x=![]() +
+![]() -2x2+4x-2,x>1,g(1)=0.g′(x)=-e2(1-x)+e2(x-1)-4x+4,
-2x2+4x-2,x>1,g(1)=0.g′(x)=-e2(1-x)+e2(x-1)-4x+4,
g″(x)=2e2(1-x)+2e2(x-1)-4≥0,∴g′(x)在(1,+∞)上單調遞增.
∴g′(x)>g′(1)=0,∴函數g(x)在(1,+∞)上單調遞增.
∴g(x)>g(1)=0,因此結論x1+x2<2成立.


科目:高中數學 來源: 題型:
【題目】某企業生產了一種新產品,在推廣期邀請了100位客戶試用該產品,每人一臺.試用一個月之后進行回訪,由客戶先對產品性能作出“滿意”或“不滿意”的評價,再讓客戶決定是否購買該試用產品(不購買則可以免費退貨,購買則僅需付成本價).經統計,決定退貨的客戶人數是總人數的一半,“對性能滿意”的客戶比“對性能不滿意”的客戶多10人,“對性能不滿意”的客戶中恰有![]() 選擇了退貨.
選擇了退貨.
(1)請完成下面的![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為“客戶購買產品與對產品性能滿意之間有關”.
的把握認為“客戶購買產品與對產品性能滿意之間有關”.
對性能滿意 | 對性能不滿意 | 合計 | |
購買產品 | |||
不購買產品 | |||
合計 |
(2)企業為了改進產品性能,現從“對性能不滿意”的客戶中按是否購買產品進行分層抽樣,隨機抽取6位客戶進行座談.座談后安排了抽獎環節,共有4張獎券,獎券上分別印有200元、400元、600元和800元字樣,抽到獎券可獲得相應獎金.6位客戶有放回的進行抽取,每人隨機抽取一張獎券,求6位客戶中購買產品的客戶人均所得獎金不少于500元的概率.
附:![]() ,其中
,其中![]()
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從8名運動員中選4人參加4×100米接力賽,在下列條件下,各有多少種不同的排法?(用數字結尾)
(1)甲、乙兩人必須跑中間兩棒;
(2)若甲、乙兩人只有一人被選且不能跑中間兩棒;
(3)若甲、乙兩人都被選且必須跑相鄰兩棒.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() 軸,直線
軸,直線![]() 交
交![]() 軸于
軸于![]() 點,
點,![]() ,
,![]() 為橢圓
為橢圓![]() 上的動點,
上的動點,![]() 的面積的最大值為1.
的面積的最大值為1.
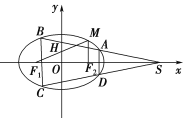
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 作兩條直線與橢圓
作兩條直線與橢圓![]() 分別交于
分別交于![]() 且使
且使![]() 軸,如圖,問四邊形
軸,如圖,問四邊形![]() 的兩條對角線的交點是否為定點?若是,求出定點的坐標;若不是,請說明理由.
的兩條對角線的交點是否為定點?若是,求出定點的坐標;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() 軸,直線
軸,直線![]() 交
交![]() 軸于
軸于![]() 點,
點,![]() ,
,![]() 為橢圓
為橢圓![]() 上的動點,
上的動點,![]() 的面積的最大值為1.
的面積的最大值為1.
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 作兩條直線與橢圓
作兩條直線與橢圓![]() 分別交于
分別交于![]() 且使
且使![]() 軸,如圖,問四邊形
軸,如圖,問四邊形![]() 的兩條對角線的交點是否為定點?若是,求出定點的坐標;若不是,請說明理由.
的兩條對角線的交點是否為定點?若是,求出定點的坐標;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】畫糖人是一種以糖為材料在石板上進行造型的民間藝術.某糖人師傅在公園內畫糖人,每天賣出某種糖人的個數與價格相關,其相關數據統計如下表:
每個糖人的價格 | 9 | 10 | 11 | 12 | 13 |
賣出糖人的個數 | 54 | 50 | 46 | 43 | 39 |
(1)根據表中數據求![]() 關于
關于![]() 的回歸直線方程;
的回歸直線方程;
(2)若該種造型的糖人的成本為2元/個,為使糖人師傅每天獲得最大利潤,則該種糖人應定價多少元?(精確到1元)
參考公式:回歸直線方程![]() ,其中
,其中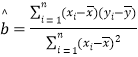 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,圓
,圓![]() ,點
,點![]() 是圓上一動點,
是圓上一動點, ![]() 的垂直平分線與
的垂直平分線與![]() 交于點
交于點![]() .
.
(1)求點![]() 的軌跡方程;
的軌跡方程;
(2)設點![]() 的軌跡為曲線
的軌跡為曲線![]() ,過點
,過點![]() 且斜率不為0的直線
且斜率不為0的直線![]() 與
與![]() 交于
交于![]() 兩點,點
兩點,點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() ,證明直線
,證明直線![]() 過定點,并求
過定點,并求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com