
【題目】如圖,橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() 軸,直線
軸,直線![]() 交
交![]() 軸于
軸于![]() 點,
點,![]() ,
,![]() 為橢圓
為橢圓![]() 上的動點,
上的動點,![]() 的面積的最大值為1.
的面積的最大值為1.
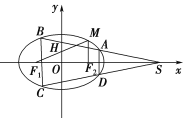
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 作兩條直線與橢圓
作兩條直線與橢圓![]() 分別交于
分別交于![]() 且使
且使![]() 軸,如圖,問四邊形
軸,如圖,問四邊形![]() 的兩條對角線的交點是否為定點?若是,求出定點的坐標;若不是,請說明理由.
的兩條對角線的交點是否為定點?若是,求出定點的坐標;若不是,請說明理由.
【答案】(1)![]() (2)定點坐標為
(2)定點坐標為![]() .
.
【解析】
(Ⅰ)![]() 意味著通徑的一半
意味著通徑的一半![]() ,
,![]() 最大面積為
最大面積為![]() ,所以
,所以![]() ,故橢圓的方程為
,故橢圓的方程為![]() .
.
(Ⅱ)根據對稱性,猜測定點必定在![]() 軸上,故可設
軸上,故可設![]() ,
,![]() ,則
,則![]() ,
,![]() ,再設
,再設![]() ,根據
,根據![]() 三點共線可以得到
三點共線可以得到![]() ,聯立直線
,聯立直線![]() 和橢圓的標準方程后消去
和橢圓的標準方程后消去![]() ,利用韋達定理可以得到
,利用韋達定理可以得到![]() ,從而
,從而![]() 過定點
過定點![]() ,同理直線
,同理直線![]() 也過
也過![]() 即兩條直線交于定點
即兩條直線交于定點![]() .
.
(Ⅰ)設![]() ,由題意可得
,由題意可得![]() ,即
,即![]() .
.
∵![]() 是
是![]() 的中位線,且
的中位線,且![]() ,
,
∴![]() ,即
,即![]() ,整理得
,整理得![]() .①
.①
又由題知,當![]() 在橢圓
在橢圓![]() 的上頂點時,
的上頂點時,![]() 的面積最大,
的面積最大,
∴![]() ,整理得
,整理得![]() ,即
,即![]() ,②
,②
聯立①②可得![]() ,變形得
,變形得![]() ,解得
,解得![]() ,進而
,進而![]() .
.
∴橢圓![]() 的方程式為
的方程式為![]() .
.
(Ⅱ)設![]() ,
,![]() ,則由對稱性可知
,則由對稱性可知![]() ,
,![]() .
.
設直線![]() 與
與![]() 軸交于點
軸交于點![]() ,直線
,直線![]() 的方程為
的方程為![]() ,
,
聯立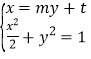 ,消去
,消去![]() ,得
,得![]() ,
,
∴![]() ,
,![]() ,
,
由![]() 三點共線
三點共線![]() ,即
,即![]() ,
,
將![]() ,
,![]() 代入整理得
代入整理得![]() ,
,
即![]() ,從而
,從而![]() ,化簡得
,化簡得![]() ,解得
,解得![]() ,于是直線
,于是直線![]() 的方程為
的方程為![]() , 故直線
, 故直線![]() 過定點
過定點![]() .同理可得
.同理可得![]() 過定點
過定點![]() ,
,
∴直線![]() 與
與![]() 的交點是定點,定點坐標為
的交點是定點,定點坐標為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 上任意一點到兩焦點
上任意一點到兩焦點![]() 距離之和為
距離之和為![]() ,離心率為
,離心率為![]() .
.
(1)求橢圓的標準方程;
(2)若直線![]() 的斜率為
的斜率為![]() ,直線
,直線![]() 與橢圓C交于
與橢圓C交于![]() 兩點.點
兩點.點![]() 為橢圓上一點,求
為橢圓上一點,求![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 定義域為
定義域為![]() ,設
,設![]() .
.
(1)試確定![]() 的取值范圍,使得函數
的取值范圍,使得函數![]() 在
在![]() 上為單調函數;
上為單調函數;
(2)求證:![]() ;
;
(3)求證:對于任意的![]() ,總存在
,總存在![]() ,滿足
,滿足![]() ,并確定這樣的
,并確定這樣的![]() 的個數.
的個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為考查某種疫苗預防疾病的效果,進行動物實驗,得到統計數據如下:
未發病 | 發病 | 總計 | |
未注射疫苗 | 20 |
|
|
注射疫苗 | 30 |
|
|
總計 | 50 | 50 | 100 |
現從所有試驗動物中任取一只,取到“注射疫苗”動物的概率為![]() .
.
(1)求![]() 列聯表中的數據
列聯表中的數據![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)能夠有多大把握認為疫苗有效?
(參考公式![]() ,
,![]() )
)
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() -x2+ef′(
-x2+ef′(![]() )x.
)x.
(Ⅰ)求f(x)的單調區間;
(Ⅱ)若存在x1,x2(x1<x2),使得f(x1)+f(x2)=1,求證:x1+x2<2.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校學生會為了解該校學生對2017年全國兩會的關注情況,隨機調查了該校200名學生,并將這200名學生分為對兩會“比較關注”與“不太關注”兩類.已知這200名學生中男生比女生多20人,對兩會“比較關注”的學生中男生人數與女生人數之比為![]() ,對兩會“不太關注”的學生中男生比女生少5人.
,對兩會“不太關注”的學生中男生比女生少5人.
(1)根據題意建立![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為男生與女生對兩會的關注有差異?
的把握認為男生與女生對兩會的關注有差異?
(2)該校學生會從對兩會“比較關注”的學生中根據性別進行分層抽樣,從中抽取7人,再從這7人中隨機選出2人進行回訪,求這2人全是男生的概率.
參考公式和數據:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在全面抗擊新冠肺炎疫情這一特殊時期,我市教育局提出“停課不停學”的口號,鼓勵學生線上學習.某校數學教師為了調查高三學生數學成績與線上學習時間之間的相關關系,對高三年級隨機選取45名學生進行跟蹤問卷,其中每周線上學習數學時間不少于5小時的有19人,余下的人中,在檢測考試中數學平均成績不足120分的占![]() ,統計成績后得到如下
,統計成績后得到如下![]() 列聯表:
列聯表:
分數不少于120分 | 分數不足120分 | 合計 | |
線上學習時間不少于5小時 | 4 | 19 | |
線上學習時間不足5小時 | |||
合計 | 45 |
(1)請完成上面![]() 列聯表;并判斷是否有99%的把握認為“高三學生的數學成績與學生線上學習時間有關”;
列聯表;并判斷是否有99%的把握認為“高三學生的數學成績與學生線上學習時間有關”;
(2)在上述樣本中從分數不少于120分的學生中,按照分層抽樣的方法,抽到線上學習時間不少于5小時和線上學習時間不足5小時的學生共5名,若在這5名學生中隨機抽取2人,求至少1人每周線上學習時間不足5小時的概率.
(下面的臨界值表供參考)
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式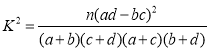 其中
其中![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com