【題目】在△ABC中，a=2，A=45°，若此三角形有兩解，則b的取值范圍是（ ）
A.（2，2 
）
B.（2，+∞）
C.（﹣∞，2）
D.（ 
， ）
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】已知數列{an}滿足a1=3，an+1﹣3an=3n（n∈N*），數列{bn}滿足bn= 
．
（Ⅰ）求證：數列{bn}是等差數列，并求數列{an}的通項公式；
（Ⅱ）求數列{an}的前n項和Sn ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】正三棱柱ABC﹣A1B1C1的棱長都為2，E，F，G為 AB，AA1 ， A1C1的中點，則B1F 與面GEF成角的正弦值（ ）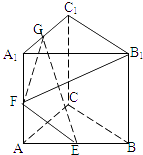
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知向量 
=（ 
sin 
，1）， 
=（cos ，cos2 ）．
（Ⅰ）若 =1，求cos（ 
﹣x）的值；
（Ⅱ）記f（x）= ，在△ABC中，A、B、C的對邊分別為a、b、c，且滿足（2a﹣c）cosB=bcosC，求函數f（A）的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校為評估新教改對教學的影響，挑選了水平相當的兩個平行班進行對比試驗。甲班采用創新教法，乙班仍采用傳統教法，一段時間后進行水平測試，成績結果全部落在
區間內（滿分100分），并繪制頻率分布直方圖如右圖，兩個班人數均為60人，成績80分及以上為優良。
根據以上信息填好下列
聯表，并判斷出有多大的把握認為學生成績優良與班級有關？
（2）以班級分層抽樣,抽取成績優良的5人參加座談，現從5人中隨機選3人來作書面發言，求發言人至少有2人來自甲班的概率。
(以下臨界值及公式僅供參考
, 
)
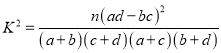查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=log2（1+x）﹣log2（1﹣x），g（x）=log2（1+x）+log2（1﹣x）．
（1）判斷函數f（x）奇偶性并證明；
（2）判斷函數f（x）單調性并用單調性定義證明；
（3）求函數g（x）的值域．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的左右焦點為
，其離心率為
，又拋物線
在點
處的切線恰好過橢圓
的一個焦點.
（1）求橢圓
的方程；
（2）過點
斜率為
的直線
交橢圓
于
兩點，直線
的斜率分別為
，是否存在常數
，使得
？若存在，求出
的值；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示的幾何體，關于其結構特征，下列說法不正確的是（ ）
A.該幾何體是由兩個同底的四棱錐組成的幾何體
B.該幾何體有12條棱、6個頂點
C.該幾何體有8個面，并且各面均為三角形
D.該幾何體有9個面，其中一個面是四邊形，其余均為三角形
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
